Private PAC Learning May be Harder than Online Learning

We continue the study of the computational complexity of differentially private PAC learning and how it is situated within the foundations of machine learning. A recent line of work uncovered a qualitative equivalence between the private PAC model and Littlestone's mistake-bounded model of online learning, in particular, showing that any concept class of Littlestone dimension $d$ can be privately PAC learned using $\mathrm{poly}(d)$ samples. This raises the natural question of whether there might be a generic conversion from online learners to private PAC learners that also preserves computational efficiency. We give a negative answer to this question under reasonable cryptographic assumptions (roughly, those from which it is possible to build indistinguishability obfuscation for all circuits). We exhibit a concept class that admits an online learner running in polynomial time with a polynomial mistake bound, but for which there is no computationally-efficient differentially private PAC learner. Our construction and analysis strengthens and generalizes that of Bun and Zhandry (TCC 2016-A), who established such a separation between private and non-private PAC learner.

Oracle-Efficient Differentially Private Learning with Public Data

Due to statistical lower bounds on the learnability of many function classes under privacy constraints, there has been recent interest in leveraging public data to improve the performance of private learning algorithms. In this model, algorithms must always guarantee differential privacy with respect to the private samples while also ensuring learning guarantees when the private data distribution is sufficiently close to that of the public data. Previous work has demonstrated that when sufficient public, unlabelled data is available, private learning can be made statistically tractable, but the resulting algorithms have all been computationally inefficient. In this work, we present the first computationally efficient, algorithms to provably leverage public data to learn privately whenever a function class is learnable non-privately, where our notion of computational efficiency is with respect to the number of calls to an optimization oracle for the function class. In addition to this general result, we provide specialized algorithms with improved sample complexities in the special cases when the function class is convex or when the task is binary classification.

Efficient Statistics for Sparse Graphical Models from Truncated Samples

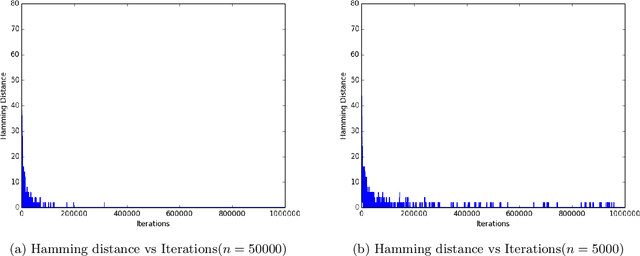
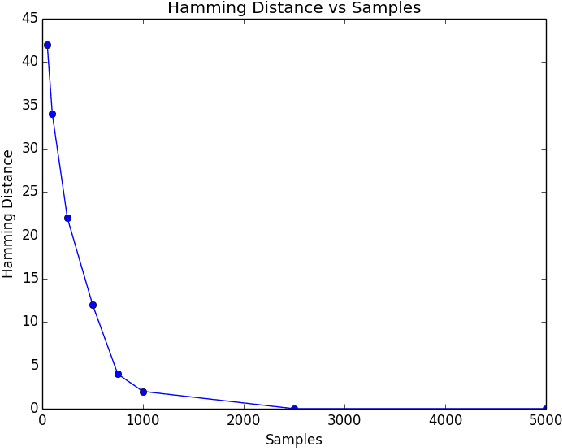
In this paper, we study high-dimensional estimation from truncated samples. We focus on two fundamental and classical problems: (i) inference of sparse Gaussian graphical models and (ii) support recovery of sparse linear models. (i) For Gaussian graphical models, suppose $d$-dimensional samples ${\bf x}$ are generated from a Gaussian $N(\mu,\Sigma)$ and observed only if they belong to a subset $S \subseteq \mathbb{R}^d$. We show that ${\mu}$ and ${\Sigma}$ can be estimated with error $\epsilon$ in the Frobenius norm, using $\tilde{O}\left(\frac{\textrm{nz}({\Sigma}^{-1})}{\epsilon^2}\right)$ samples from a truncated $\mathcal{N}({\mu},{\Sigma})$ and having access to a membership oracle for $S$. The set $S$ is assumed to have non-trivial measure under the unknown distribution but is otherwise arbitrary. (ii) For sparse linear regression, suppose samples $({\bf x},y)$ are generated where $y = {\bf x}^\top{{\Omega}^*} + \mathcal{N}(0,1)$ and $({\bf x}, y)$ is seen only if $y$ belongs to a truncation set $S \subseteq \mathbb{R}$. We consider the case that ${\Omega}^*$ is sparse with a support set of size $k$. Our main result is to establish precise conditions on the problem dimension $d$, the support size $k$, the number of observations $n$, and properties of the samples and the truncation that are sufficient to recover the support of ${\Omega}^*$. Specifically, we show that under some mild assumptions, only $O(k^2 \log d)$ samples are needed to estimate ${\Omega}^*$ in the $\ell_\infty$-norm up to a bounded error. For both problems, our estimator minimizes the sum of the finite population negative log-likelihood function and an $\ell_1$-regularization term.

Quantifying Error in the Presence of Confounders for Causal Inference

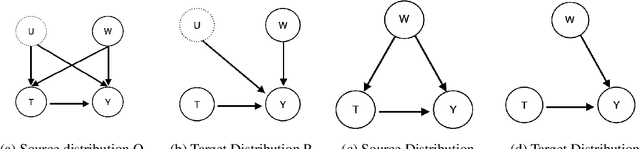
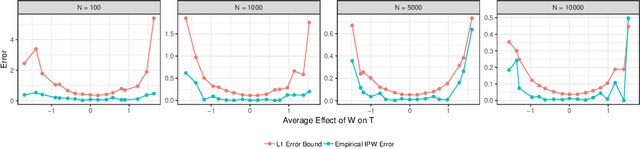
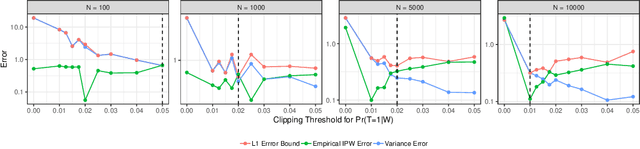
Estimating average causal effect (ACE) is useful whenever we want to know the effect of an intervention on a given outcome. In the absence of a randomized experiment, many methods such as stratification and inverse propensity weighting have been proposed to estimate ACE. However, it is hard to know which method is optimal for a given dataset or which hyperparameters to use for a chosen method. To this end, we provide a framework to characterize the loss of a causal inference method against the true ACE, by framing causal inference as a representation learning problem. We show that many popular methods, including back-door methods can be considered as weighting or representation learning algorithms, and provide general error bounds for their causal estimates. In addition, we consider the case when unobserved variables can confound the causal estimate and extend proposed bounds using principles of robust statistics, considering confounding as contamination under the Huber contamination model. These bounds are also estimable; as an example, we provide empirical bounds for the Inverse Propensity Weighting (IPW) estimator and show how the bounds can be used to optimize the threshold of clipping extreme propensity scores. Our work provides a new way to reason about competing estimators, and opens up the potential of deriving new methods by minimizing the proposed error bounds.