Enhancing Watermarked Language Models to Identify Users

A zero-bit watermarked language model produces text that is indistinguishable from that of the underlying model, but which can be detected as machine-generated using a secret key. But merely detecting AI-generated spam, say, as watermarked may not prevent future abuses. If we could additionally trace the text to a spammer's API token, we could then cut off their access to the model. We introduce multi-user watermarks, which allow tracing model-generated text to individuals or to groups of colluding users. We construct multi-user watermarking schemes from undetectable zero-bit watermarking schemes. Importantly, our schemes provide both zero-bit and multi-user assurances at the same time: detecting shorter snippets as well as the original scheme and tracing longer excerpts to individuals. Along the way, we give a generic construction of a watermarking scheme that embeds long messages into generated text. Ours are the first black-box reductions between watermarking schemes for language models. A major challenge for black-box reductions is the lack of a unified abstraction for robustness -- that marked text is detectable after edits. Existing works give incomparable robustness guarantees, based on bespoke requirements on the language model's outputs and the users' edits. We introduce a new abstraction -- AEB-robustness -- to overcome this challenge. AEB-robustness provides that the watermark is detectable whenever the edited text "approximates enough blocks" of model-generated output. Specifying the robustness condition amounts to defining approximates, enough, and blocks. Using our new abstraction, we relate the robustness properties of our constructions to that of the underlying zero-bit scheme. Whereas prior works only guarantee robustness for a single text generated in response to a single prompt, our schemes are robust against adaptive prompting, a stronger adversarial model.

Private PAC Learning May be Harder than Online Learning

We continue the study of the computational complexity of differentially private PAC learning and how it is situated within the foundations of machine learning. A recent line of work uncovered a qualitative equivalence between the private PAC model and Littlestone's mistake-bounded model of online learning, in particular, showing that any concept class of Littlestone dimension $d$ can be privately PAC learned using $\mathrm{poly}(d)$ samples. This raises the natural question of whether there might be a generic conversion from online learners to private PAC learners that also preserves computational efficiency. We give a negative answer to this question under reasonable cryptographic assumptions (roughly, those from which it is possible to build indistinguishability obfuscation for all circuits). We exhibit a concept class that admits an online learner running in polynomial time with a polynomial mistake bound, but for which there is no computationally-efficient differentially private PAC learner. Our construction and analysis strengthens and generalizes that of Bun and Zhandry (TCC 2016-A), who established such a separation between private and non-private PAC learner.

From Soft Classifiers to Hard Decisions: How fair can we be?

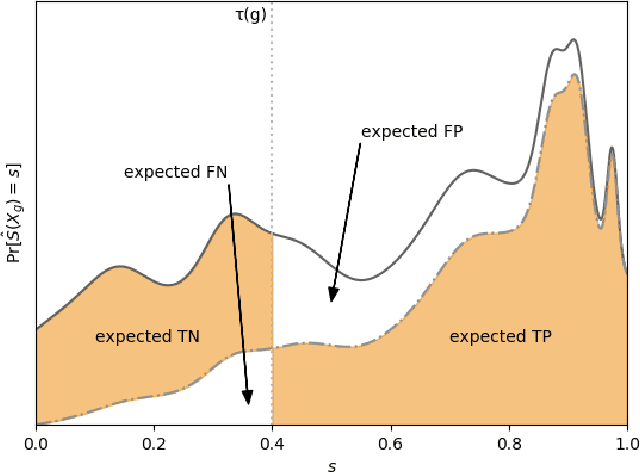
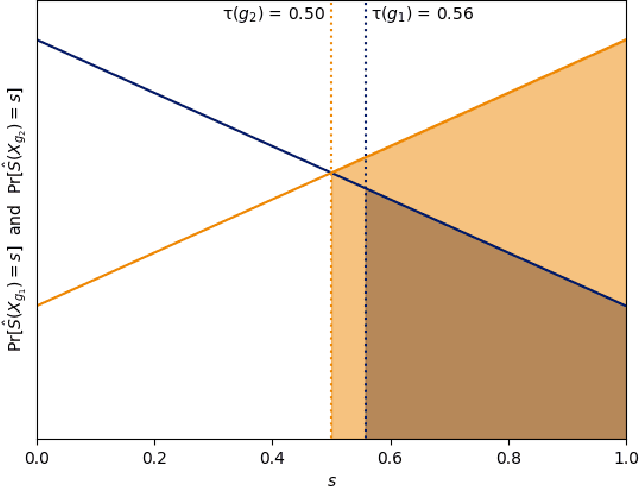
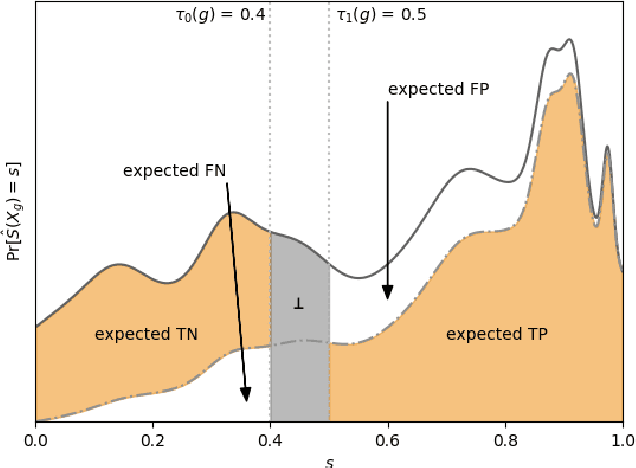
A popular methodology for building binary decision-making classifiers in the presence of imperfect information is to first construct a non-binary "scoring" classifier that is calibrated over all protected groups, and then to post-process this score to obtain a binary decision. We study the feasibility of achieving various fairness properties by post-processing calibrated scores, and then show that deferring post-processors allow for more fairness conditions to hold on the final decision. Specifically, we show: 1. There does not exist a general way to post-process a calibrated classifier to equalize protected groups' positive or negative predictive value (PPV or NPV). For certain "nice" calibrated classifiers, either PPV or NPV can be equalized when the post-processor uses different thresholds across protected groups, though there exist distributions of calibrated scores for which the two measures cannot be both equalized. When the post-processing consists of a single global threshold across all groups, natural fairness properties, such as equalizing PPV in a nontrivial way, do not hold even for "nice" classifiers. 2. When the post-processing is allowed to `defer' on some decisions (that is, to avoid making a decision by handing off some examples to a separate process), then for the non-deferred decisions, the resulting classifier can be made to equalize PPV, NPV, false positive rate (FPR) and false negative rate (FNR) across the protected groups. This suggests a way to partially evade the impossibility results of Chouldechova and Kleinberg et al., which preclude equalizing all of these measures simultaneously. We also present different deferring strategies and show how they affect the fairness properties of the overall system. We evaluate our post-processing techniques using the COMPAS data set from 2016.