S-CFE: Simple Counterfactual Explanations

We study the problem of finding optimal sparse, manifold-aligned counterfactual explanations for classifiers. Canonically, this can be formulated as an optimization problem with multiple non-convex components, including classifier loss functions and manifold alignment (or \emph{plausibility}) metrics. The added complexity of enforcing \emph{sparsity}, or shorter explanations, complicates the problem further. Existing methods often focus on specific models and plausibility measures, relying on convex $\ell_1$ regularizers to enforce sparsity. In this paper, we tackle the canonical formulation using the accelerated proximal gradient (APG) method, a simple yet efficient first-order procedure capable of handling smooth non-convex objectives and non-smooth $\ell_p$ (where $0 \leq p < 1$) regularizers. This enables our approach to seamlessly incorporate various classifiers and plausibility measures while producing sparser solutions. Our algorithm only requires differentiable data-manifold regularizers and supports box constraints for bounded feature ranges, ensuring the generated counterfactuals remain \emph{actionable}. Finally, experiments on real-world datasets demonstrate that our approach effectively produces sparse, manifold-aligned counterfactual explanations while maintaining proximity to the factual data and computational efficiency.

The Good, the Bad and the Ugly: Watermarks, Transferable Attacks and Adversarial Defenses

We formalize and extend existing definitions of backdoor-based watermarks and adversarial defenses as interactive protocols between two players. The existence of these schemes is inherently tied to the learning tasks for which they are designed. Our main result shows that for almost every discriminative learning task, at least one of the two -- a watermark or an adversarial defense -- exists. The term "almost every" indicates that we also identify a third, counterintuitive but necessary option, i.e., a scheme we call a transferable attack. By transferable attack, we refer to an efficient algorithm computing queries that look indistinguishable from the data distribution and fool all efficient defenders. To this end, we prove the necessity of a transferable attack via a construction that uses a cryptographic tool called homomorphic encryption. Furthermore, we show that any task that satisfies our notion of a transferable attack implies a cryptographic primitive, thus requiring the underlying task to be computationally complex. These two facts imply an "equivalence" between the existence of transferable attacks and cryptography. Finally, we show that the class of tasks of bounded VC-dimension has an adversarial defense, and a subclass of them has a watermark.

An Analysis of $D^α$ seeding for $k$-means

One of the most popular clustering algorithms is the celebrated $D^\alpha$ seeding algorithm (also know as $k$-means++ when $\alpha=2$) by Arthur and Vassilvitskii (2007), who showed that it guarantees in expectation an $O(2^{2\alpha}\cdot \log k)$-approximate solution to the ($k$,$\alpha$)-means cost (where euclidean distances are raised to the power $\alpha$) for any $\alpha\ge 1$. More recently, Balcan, Dick, and White (2018) observed experimentally that using $D^\alpha$ seeding with $\alpha>2$ can lead to a better solution with respect to the standard $k$-means objective (i.e. the $(k,2)$-means cost). In this paper, we provide a rigorous understanding of this phenomenon. For any $\alpha>2$, we show that $D^\alpha$ seeding guarantees in expectation an approximation factor of $$ O_\alpha \left((g_\alpha)^{2/\alpha}\cdot \left(\frac{\sigma_{\mathrm{max}}}{\sigma_{\mathrm{min}}}\right)^{2-4/\alpha}\cdot (\min\{\ell,\log k\})^{2/\alpha}\right)$$ with respect to the standard $k$-means cost of any underlying clustering; where $g_\alpha$ is a parameter capturing the concentration of the points in each cluster, $\sigma_{\mathrm{max}}$ and $\sigma_{\mathrm{min}}$ are the maximum and minimum standard deviation of the clusters around their means, and $\ell$ is the number of distinct mixing weights in the underlying clustering (after rounding them to the nearest power of $2$). We complement these results by some lower bounds showing that the dependency on $g_\alpha$ and $\sigma_{\mathrm{max}}/\sigma_{\mathrm{min}}$ is tight. Finally, we provide an experimental confirmation of the effects of the aforementioned parameters when using $D^\alpha$ seeding. Further, we corroborate the observation that $\alpha>2$ can indeed improve the $k$-means cost compared to $D^2$ seeding, and that this advantage remains even if we run Lloyd's algorithm after the seeding.

Efficient Statistics for Sparse Graphical Models from Truncated Samples

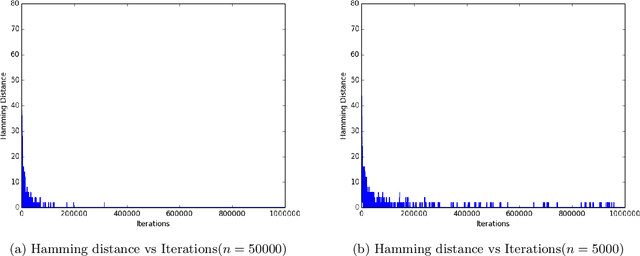
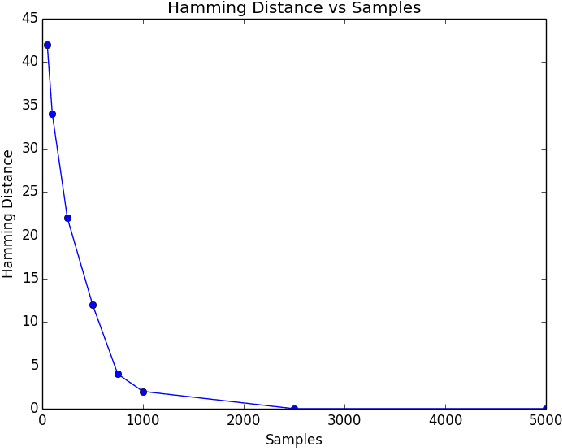
In this paper, we study high-dimensional estimation from truncated samples. We focus on two fundamental and classical problems: (i) inference of sparse Gaussian graphical models and (ii) support recovery of sparse linear models. (i) For Gaussian graphical models, suppose $d$-dimensional samples ${\bf x}$ are generated from a Gaussian $N(\mu,\Sigma)$ and observed only if they belong to a subset $S \subseteq \mathbb{R}^d$. We show that ${\mu}$ and ${\Sigma}$ can be estimated with error $\epsilon$ in the Frobenius norm, using $\tilde{O}\left(\frac{\textrm{nz}({\Sigma}^{-1})}{\epsilon^2}\right)$ samples from a truncated $\mathcal{N}({\mu},{\Sigma})$ and having access to a membership oracle for $S$. The set $S$ is assumed to have non-trivial measure under the unknown distribution but is otherwise arbitrary. (ii) For sparse linear regression, suppose samples $({\bf x},y)$ are generated where $y = {\bf x}^\top{{\Omega}^*} + \mathcal{N}(0,1)$ and $({\bf x}, y)$ is seen only if $y$ belongs to a truncation set $S \subseteq \mathbb{R}$. We consider the case that ${\Omega}^*$ is sparse with a support set of size $k$. Our main result is to establish precise conditions on the problem dimension $d$, the support size $k$, the number of observations $n$, and properties of the samples and the truncation that are sufficient to recover the support of ${\Omega}^*$. Specifically, we show that under some mild assumptions, only $O(k^2 \log d)$ samples are needed to estimate ${\Omega}^*$ in the $\ell_\infty$-norm up to a bounded error. For both problems, our estimator minimizes the sum of the finite population negative log-likelihood function and an $\ell_1$-regularization term.

Better Depth-Width Trade-offs for Neural Networks through the lens of Dynamical Systems

The expressivity of neural networks as a function of their depth, width and type of activation units has been an important question in deep learning theory. Recently, depth separation results for ReLU networks were obtained via a new connection with dynamical systems, using a generalized notion of fixed points of a continuous map $f$, called periodic points. In this work, we strengthen the connection with dynamical systems and we improve the existing width lower bounds along several aspects. Our first main result is period-specific width lower bounds that hold under the stronger notion of $L^1$-approximation error, instead of the weaker classification error. Our second contribution is that we provide sharper width lower bounds, still yielding meaningful exponential depth-width separations, in regimes where previous results wouldn't apply. A byproduct of our results is that there exists a universal constant characterizing the depth-width trade-offs, as long as $f$ has odd periods. Technically, our results follow by unveiling a tighter connection between the following three quantities of a given function: its period, its Lipschitz constant and the growth rate of the number of oscillations arising under compositions of the function $f$ with itself.

Last iterate convergence in no-regret learning: constrained min-max optimization for convex-concave landscapes

In a recent series of papers it has been established that variants of Gradient Descent/Ascent and Mirror Descent exhibit last iterate convergence in convex-concave zero-sum games. Specifically, \cite{DISZ17, LiangS18} show last iterate convergence of the so called "Optimistic Gradient Descent/Ascent" for the case of \textit{unconstrained} min-max optimization. Moreover, in \cite{Metal} the authors show that Mirror Descent with an extra gradient step displays last iterate convergence for convex-concave problems (both constrained and unconstrained), though their algorithm does not follow the online learning framework; it uses extra information rather than \textit{only} the history to compute the next iteration. In this work, we show that "Optimistic Multiplicative-Weights Update (OMWU)" which follows the no-regret online learning framework, exhibits last iterate convergence locally for convex-concave games, generalizing the results of \cite{DP19} where last iterate convergence of OMWU was shown only for the \textit{bilinear case}. We complement our results with experiments that indicate fast convergence of the method.

Depth-Width Trade-offs for ReLU Networks via Sharkovsky's Theorem

Understanding the representational power of Deep Neural Networks (DNNs) and how their structural properties (e.g., depth, width, type of activation unit) affect the functions they can compute, has been an important yet challenging question in deep learning and approximation theory. In a seminal paper, Telgarsky highlighted the benefits of depth by presenting a family of functions (based on simple triangular waves) for which DNNs achieve zero classification error, whereas shallow networks with fewer than exponentially many nodes incur constant error. Even though Telgarsky's work reveals the limitations of shallow neural networks, it does not inform us on why these functions are difficult to represent and in fact he states it as a tantalizing open question to characterize those functions that cannot be well-approximated by smaller depths. In this work, we point to a new connection between DNNs expressivity and Sharkovsky's Theorem from dynamical systems, that enables us to characterize the depth-width trade-offs of ReLU networks for representing functions based on the presence of generalized notion of fixed points, called periodic points (a fixed point is a point of period 1). Motivated by our observation that the triangle waves used in Telgarsky's work contain points of period 3 - a period that is special in that it implies chaotic behavior based on the celebrated result by Li-Yorke - we proceed to give general lower bounds for the width needed to represent periodic functions as a function of the depth. Technically, the crux of our approach is based on an eigenvalue analysis of the dynamical system associated with such functions.

On the Convergence of EM for truncated mixtures of two Gaussians

Motivated by a recent result of Daskalakis et al. \cite{DGTZ18}, we analyze the population version of Expectation-Maximization (EM) algorithm for the case of \textit{truncated} mixtures of two Gaussians. Truncated samples from a $d$-dimensional mixture of two Gaussians $\frac{1}{2} \mathcal{N}(\vec{\mu}, \vec{\Sigma})+ \frac{1}{2} \mathcal{N}(-\vec{\mu}, \vec{\Sigma})$ means that a sample is only revealed if it falls in some subset $S \subset \mathbb{R}^d$ of positive (Lebesgue) measure. We show that for $d=1$, EM converges almost surely (under random initialization) to the true mean (variance $\sigma^2$ is known) for any measurable set $S$. Moreover, for $d>1$ we show EM almost surely converges to the true mean $\vec{\mu}$ for any measurable set $S$, under the assumption that the map of EM has only three fixed points, namely $-\vec{\mu}, \vec{0}, \vec{\mu}$ (covariance matrix $\vec{\Sigma}$ is known). Our techniques deviate from those of Daskalakis et al. \cite{DTZ17}, which heavily depend on symmetry that the untruncated problem exhibits. The fact that the truncated set $S$ may not be symmetric around $\vec{0}$ makes it impossible to compute a closed form of the update rule of EM. We circumvent this fact by using techniques from dynamical systems, in particular implicit function theorem and stability analysis around the fixed points of the update rule of EM.