Efficient Statistics for Sparse Graphical Models from Truncated Samples
Paper and Code
Jun 17, 2020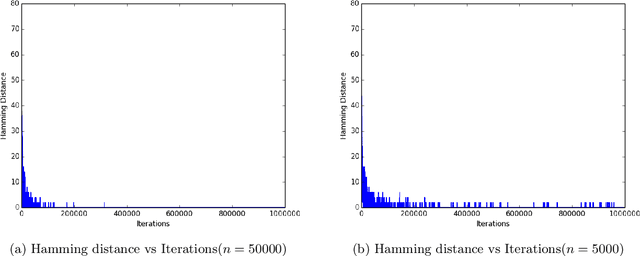
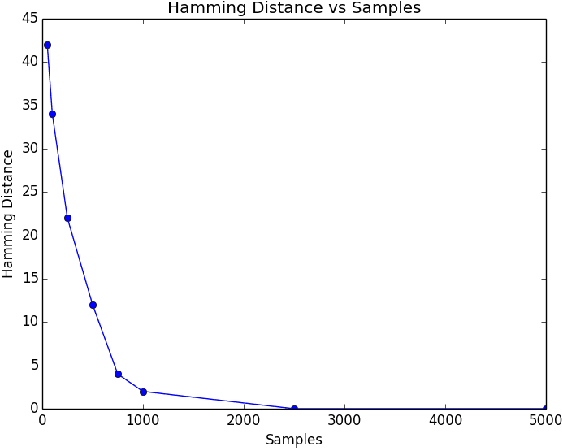
In this paper, we study high-dimensional estimation from truncated samples. We focus on two fundamental and classical problems: (i) inference of sparse Gaussian graphical models and (ii) support recovery of sparse linear models. (i) For Gaussian graphical models, suppose $d$-dimensional samples ${\bf x}$ are generated from a Gaussian $N(\mu,\Sigma)$ and observed only if they belong to a subset $S \subseteq \mathbb{R}^d$. We show that ${\mu}$ and ${\Sigma}$ can be estimated with error $\epsilon$ in the Frobenius norm, using $\tilde{O}\left(\frac{\textrm{nz}({\Sigma}^{-1})}{\epsilon^2}\right)$ samples from a truncated $\mathcal{N}({\mu},{\Sigma})$ and having access to a membership oracle for $S$. The set $S$ is assumed to have non-trivial measure under the unknown distribution but is otherwise arbitrary. (ii) For sparse linear regression, suppose samples $({\bf x},y)$ are generated where $y = {\bf x}^\top{{\Omega}^*} + \mathcal{N}(0,1)$ and $({\bf x}, y)$ is seen only if $y$ belongs to a truncation set $S \subseteq \mathbb{R}$. We consider the case that ${\Omega}^*$ is sparse with a support set of size $k$. Our main result is to establish precise conditions on the problem dimension $d$, the support size $k$, the number of observations $n$, and properties of the samples and the truncation that are sufficient to recover the support of ${\Omega}^*$. Specifically, we show that under some mild assumptions, only $O(k^2 \log d)$ samples are needed to estimate ${\Omega}^*$ in the $\ell_\infty$-norm up to a bounded error. For both problems, our estimator minimizes the sum of the finite population negative log-likelihood function and an $\ell_1$-regularization term.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge