The Good, the Bad and the Ugly: Watermarks, Transferable Attacks and Adversarial Defenses

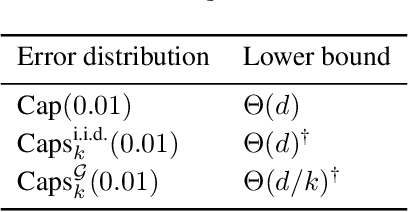
We formalize and extend existing definitions of backdoor-based watermarks and adversarial defenses as interactive protocols between two players. The existence of these schemes is inherently tied to the learning tasks for which they are designed. Our main result shows that for almost every discriminative learning task, at least one of the two -- a watermark or an adversarial defense -- exists. The term "almost every" indicates that we also identify a third, counterintuitive but necessary option, i.e., a scheme we call a transferable attack. By transferable attack, we refer to an efficient algorithm computing queries that look indistinguishable from the data distribution and fool all efficient defenders. To this end, we prove the necessity of a transferable attack via a construction that uses a cryptographic tool called homomorphic encryption. Furthermore, we show that any task that satisfies our notion of a transferable attack implies a cryptographic primitive, thus requiring the underlying task to be computationally complex. These two facts imply an "equivalence" between the existence of transferable attacks and cryptography. Finally, we show that the class of tasks of bounded VC-dimension has an adversarial defense, and a subclass of them has a watermark.

Bayes Complexity of Learners vs Overfitting

We introduce a new notion of complexity of functions and we show that it has the following properties: (i) it governs a PAC Bayes-like generalization bound, (ii) for neural networks it relates to natural notions of complexity of functions (such as the variation), and (iii) it explains the generalization gap between neural networks and linear schemes. While there is a large set of papers which describes bounds that have each such property in isolation, and even some that have two, as far as we know, this is a first notion that satisfies all three of them. Moreover, in contrast to previous works, our notion naturally generalizes to neural networks with several layers. Even though the computation of our complexity is nontrivial in general, an upper-bound is often easy to derive, even for higher number of layers and functions with structure, such as period functions. An upper-bound we derive allows to show a separation in the number of samples needed for good generalization between 2 and 4-layer neural networks for periodic functions.

Provable Adversarial Robustness in the Quantum Model

Modern machine learning systems have been applied successfully to a variety of tasks in recent years but making such systems robust against adversarially chosen modifications of input instances seems to be a much harder problem. It is probably fair to say that no fully satisfying solution has been found up to date and it is not clear if the standard formulation even allows for a principled solution. Hence, rather than following the classical path of bounded perturbations, we consider a model similar to the quantum PAC-learning model introduced by Bshouty and Jackson [1995]. Our first key contribution shows that in this model we can reduce adversarial robustness to the conjunction of two classical learning theory problems, namely (Problem 1) the problem of finding generative models and (Problem 2) the problem of devising classifiers that are robust with respect to distributional shifts. Our second key contribution is that the considered framework does not rely on specific (and hence also somewhat arbitrary) threat models like $\ell_p$ bounded perturbations. Instead, our reduction guarantees that in order to solve the adversarial robustness problem in our model it suffices to consider a single distance notion, i.e. the Hellinger distance. From the technical perspective our protocols are heavily based on the recent advances on delegation of quantum computation, e.g. Mahadev [2018]. Although the considered model is quantum and therefore not immediately applicable to ``real-world'' situations, one might hope that in the future either one can find a way to embed ``real-world'' problems into a quantum framework or that classical algorithms can be found that are capable of mimicking their powerful quantum counterparts.

Noether: The More Things Change, the More Stay the Same

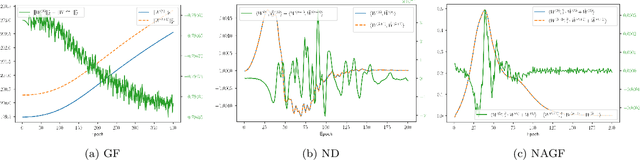
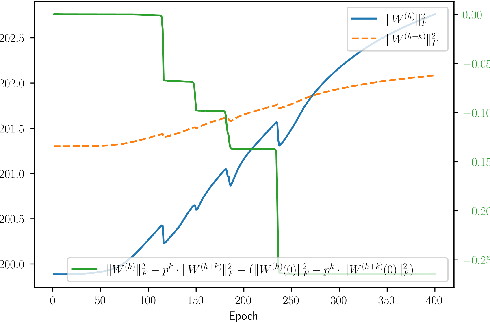
Symmetries have proven to be important ingredients in the analysis of neural networks. So far their use has mostly been implicit or seemingly coincidental. We undertake a systematic study of the role that symmetry plays. In particular, we clarify how symmetry interacts with the learning algorithm. The key ingredient in our study is played by Noether's celebrated theorem which, informally speaking, states that symmetry leads to conserved quantities (e.g., conservation of energy or conservation of momentum). In the realm of neural networks under gradient descent, model symmetries imply restrictions on the gradient path. E.g., we show that symmetry of activation functions leads to boundedness of weight matrices, for the specific case of linear activations it leads to balance equations of consecutive layers, data augmentation leads to gradient paths that have "momentum"-type restrictions, and time symmetry leads to a version of the Neural Tangent Kernel. Symmetry alone does not specify the optimization path, but the more symmetries are contained in the model the more restrictions are imposed on the path. Since symmetry also implies over-parametrization, this in effect implies that some part of this over-parametrization is cancelled out by the existence of the conserved quantities. Symmetry can therefore be thought of as one further important tool in understanding the performance of neural networks under gradient descent.

Adversarial Robustness: What fools you makes you stronger

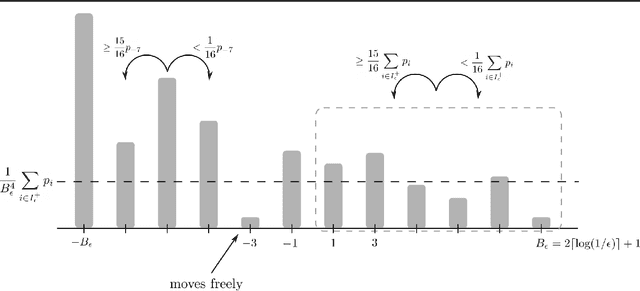
We prove an exponential separation for the sample complexity between the standard PAC-learning model and a version of the Equivalence-Query-learning model. We then show that this separation has interesting implications for adversarial robustness. We explore a vision of designing an adaptive defense that in the presence of an attacker computes a model that is provably robust. In particular, we show how to realize this vision in a simplified setting. In order to do so, we introduce a notion of a strong adversary: he is not limited by the type of perturbations he can apply but when presented with a classifier can repetitively generate different adversarial examples. We explain why this notion is interesting to study and use it to prove the following. There exists an efficient adversarial-learning-like scheme such that for every strong adversary $\mathbf{A}$ it outputs a classifier that (a) cannot be strongly attacked by $\mathbf{A}$, or (b) has error at most $\epsilon$. In both cases our scheme uses exponentially (in $\epsilon$) fewer samples than what the PAC bound requires.

Query complexity of adversarial attacks

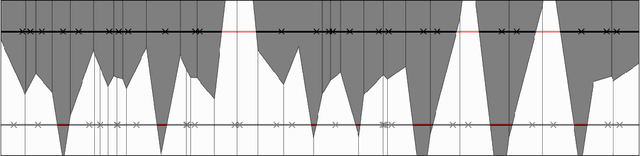
Modern machine learning models are typically highly accurate but have been shown to be vulnerable to small, adversarially-chosen perturbations of the input. There are two main models of attacks considered in the literature: black-box and white-box. We consider these threat models as two ends of a fine-grained spectrum, indexed by the number of queries the adversary can ask. Using this point of view we investigate how many queries the adversary needs to make to design an attack that is comparable to the best possible attack in the white-box model. We analyze two classical learning algorithms on two synthetic tasks for which we prove meaningful security guarantees. The obtained bounds suggest that some learning algorithms are inherently more robust against query-bounded adversaries than others.

Constructing a provably adversarially-robust classifier from a high accuracy one

Modern machine learning models with very high accuracy have been shown to be vulnerable to small, adversarially chosen perturbations of the input. Given black-box access to a high-accuracy classifier $f$, we show how to construct a new classifier $g$ that has high accuracy and is also robust to adversarial $\ell_2$-bounded perturbations. Our algorithm builds upon the framework of \textit{randomized smoothing} that has been recently shown to outperform all previous defenses against $\ell_2$-bounded adversaries. Using techniques like random partitions and doubling dimension, we are able to bound the adversarial error of $g$ in terms of the optimum error. In this paper we focus on our conceptual contribution, but we do present two examples to illustrate our framework. We will argue that, under some assumptions, our bounds are optimal for these cases.