Quantifying Error in the Presence of Confounders for Causal Inference

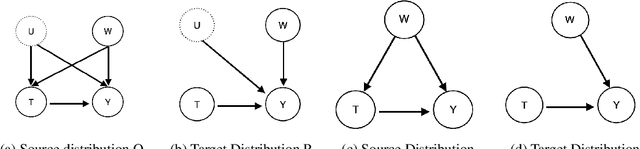
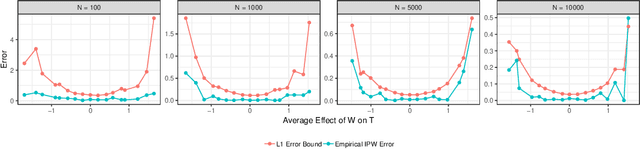
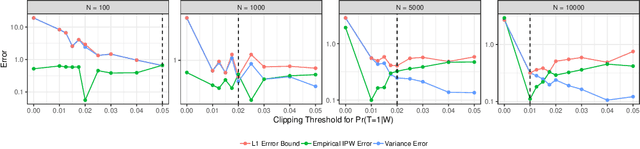
Estimating average causal effect (ACE) is useful whenever we want to know the effect of an intervention on a given outcome. In the absence of a randomized experiment, many methods such as stratification and inverse propensity weighting have been proposed to estimate ACE. However, it is hard to know which method is optimal for a given dataset or which hyperparameters to use for a chosen method. To this end, we provide a framework to characterize the loss of a causal inference method against the true ACE, by framing causal inference as a representation learning problem. We show that many popular methods, including back-door methods can be considered as weighting or representation learning algorithms, and provide general error bounds for their causal estimates. In addition, we consider the case when unobserved variables can confound the causal estimate and extend proposed bounds using principles of robust statistics, considering confounding as contamination under the Huber contamination model. These bounds are also estimable; as an example, we provide empirical bounds for the Inverse Propensity Weighting (IPW) estimator and show how the bounds can be used to optimize the threshold of clipping extreme propensity scores. Our work provides a new way to reason about competing estimators, and opens up the potential of deriving new methods by minimizing the proposed error bounds.