Convergence and sample complexity of gradient methods for the model-free linear quadratic regulator problem

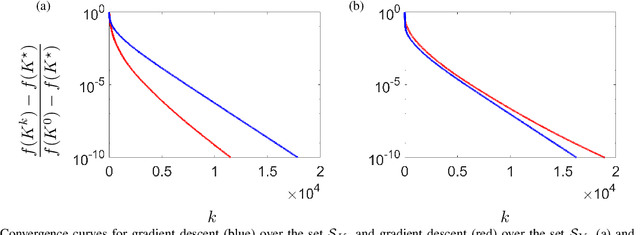
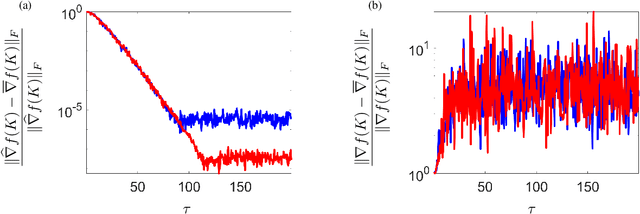
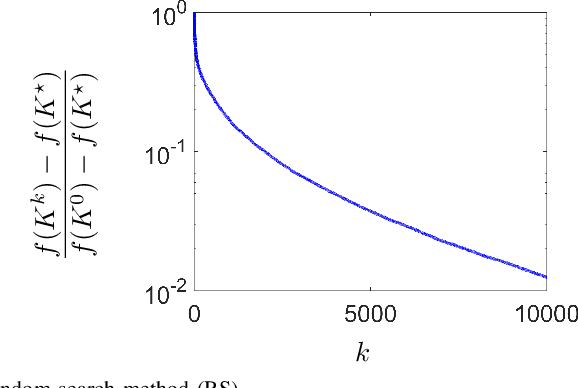
Model-free reinforcement learning attempts to find an optimal control action for an unknown dynamical system by directly searching over the parameter space of controllers. The convergence behavior and statistical properties of these approaches are often poorly understood because of the nonconvex nature of the underlying optimization problems as well as the lack of exact gradient computation. In this paper, we take a step towards demystifying the performance and efficiency of such methods by focusing on the standard infinite-horizon linear quadratic regulator problem for continuous-time systems with unknown state-space parameters. We establish exponential stability for the ordinary differential equation (ODE) that governs the gradient-flow dynamics over the set of stabilizing feedback gains and show that a similar result holds for the gradient descent method that arises from the forward Euler discretization of the corresponding ODE. We also provide theoretical bounds on the convergence rate and sample complexity of a random search method. Our results demonstrate that the required simulation time for achieving $\epsilon$-accuracy in a model-free setup and the total number of function evaluations both scale as $\log \, (1/\epsilon)$.