Convergence and sample complexity of gradient methods for the model-free linear quadratic regulator problem

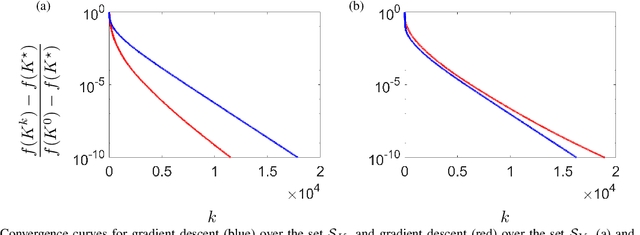
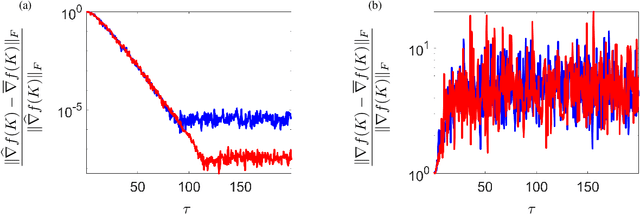
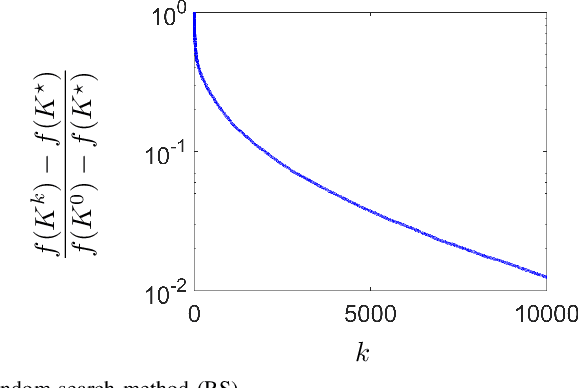
Model-free reinforcement learning attempts to find an optimal control action for an unknown dynamical system by directly searching over the parameter space of controllers. The convergence behavior and statistical properties of these approaches are often poorly understood because of the nonconvex nature of the underlying optimization problems as well as the lack of exact gradient computation. In this paper, we take a step towards demystifying the performance and efficiency of such methods by focusing on the standard infinite-horizon linear quadratic regulator problem for continuous-time systems with unknown state-space parameters. We establish exponential stability for the ordinary differential equation (ODE) that governs the gradient-flow dynamics over the set of stabilizing feedback gains and show that a similar result holds for the gradient descent method that arises from the forward Euler discretization of the corresponding ODE. We also provide theoretical bounds on the convergence rate and sample complexity of a random search method. Our results demonstrate that the required simulation time for achieving $\epsilon$-accuracy in a model-free setup and the total number of function evaluations both scale as $\log \, (1/\epsilon)$.

Stochastic dynamical modeling of turbulent flows

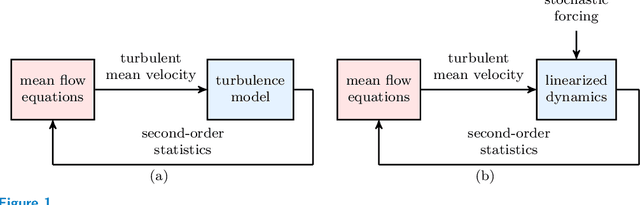
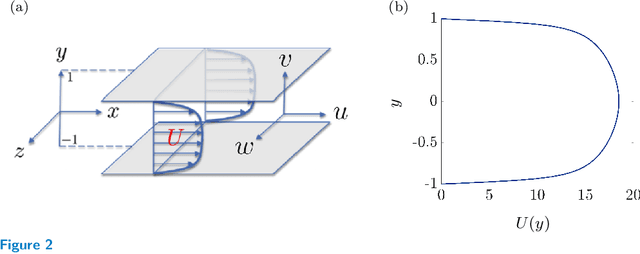
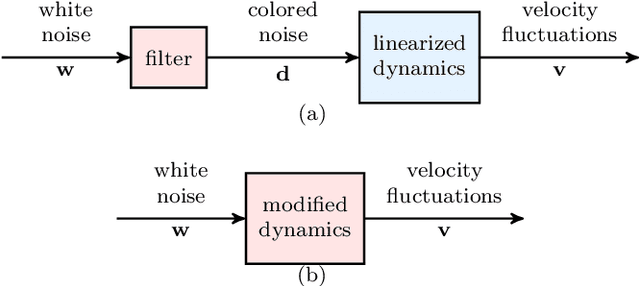
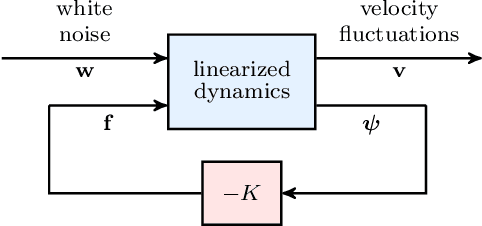
Advanced measurement techniques and high performance computing have made large data sets available for a wide range of turbulent flows that arise in engineering applications. Drawing on this abundance of data, dynamical models can be constructed to reproduce structural and statistical features of turbulent flows, opening the way to the design of effective model-based flow control strategies. This review describes a framework for completing second-order statistics of turbulent flows by models that are based on the Navier-Stokes equations linearized around the turbulent mean velocity. Systems theory and convex optimization are combined to address the inherent uncertainty in the dynamics and the statistics of the flow by seeking a suitable parsimonious correction to the prior linearized model. Specifically, dynamical couplings between states of the linearized model dictate structural constraints on the statistics of flow fluctuations. Thence, colored-in-time stochastic forcing that drives the linearized model is sought to account for and reconcile dynamics with available data (i.e., partially known second order statistics). The number of dynamical degrees of freedom that are directly affected by stochastic excitation is minimized as a measure of model parsimony. The spectral content of the resulting colored-in-time stochastic contribution can alternatively be seen to arise from a low-rank structural perturbation of the linearized dynamical generator, pointing to suitable dynamical corrections that may account for the absence of the nonlinear interactions in the linearized model.

Proximal algorithms for large-scale statistical modeling and optimal sensor/actuator selection

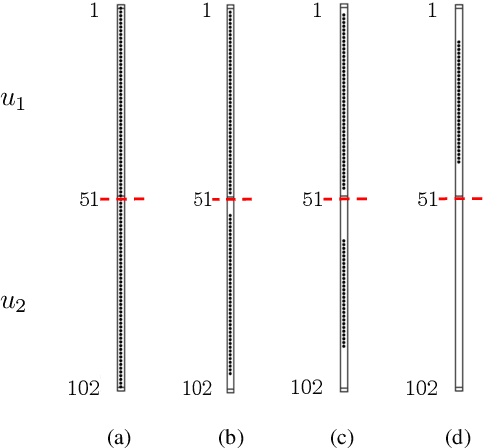
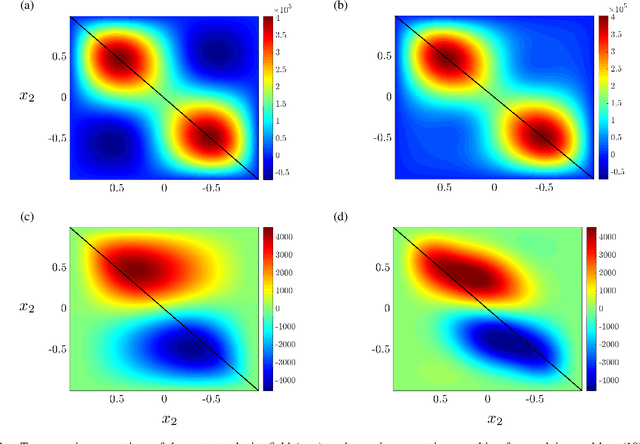
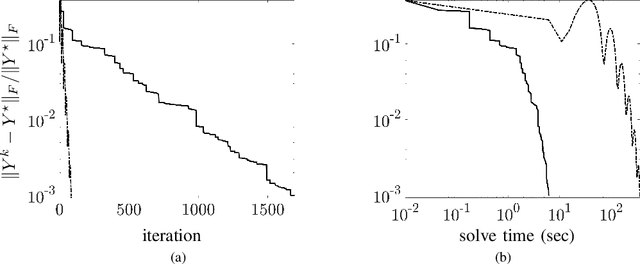
Several problems in modeling and control of stochastically-driven dynamical systems can be cast as regularized semi-definite programs. We examine two such representative problems and show that they can be formulated in a similar manner. The first, in statistical modeling, seeks to reconcile observed statistics by suitably and minimally perturbing prior dynamics. The second, seeks to optimally select sensors and actuators for control purposes. To address modeling and control of large-scale systems we develop a unified algorithmic framework using proximal methods. Our customized algorithms exploit problem structure and allow handling statistical modeling, as well as sensor and actuator selection, for substantially larger scales than what is amenable to current general-purpose solvers.