Data Assimilation for Sign-indefinite Priors: A generalization of Sinkhorn's algorithm

The purpose of this work is to develop a framework to calibrate signed datasets so as to be consistent with specified marginals by suitably extending the Schr\"odinger-Fortet-Sinkhorn paradigm. Specifically, we seek to revise sign-indefinite multi-dimensional arrays in a way that the updated values agree with specified marginals. Our approach follows the rationale in Schr\"odinger's problem, aimed at updating a "prior" probability measure to agree with marginal distributions. The celebrated Sinkhorn's algorithm (established earlier by R.\ Fortet) that solves Schr\"odinger's problem found early applications in calibrating contingency tables in statistics and, more recently, multi-marginal problems in machine learning and optimal transport. Herein, we postulate a sign-indefinite prior in the form of a multi-dimensional array, and propose an optimization problem to suitably update this prior to ensure consistency with given marginals. The resulting algorithm generalizes the Sinkhorn algorithm in that it amounts to iterative scaling of the entries of the array along different coordinate directions. The scaling is multiplicative but also, in contrast to Sinkhorn, inverse-multiplicative depending on the sign of the entries. Our algorithm reduces to the classical Sinkhorn algorithm when the entries of the prior are positive.

Negative probabilities in Gene Regulatory Networks

We introduce a natural framework to identify sign-indefinite co-expressions between genes based on the known expressions and given the sign of their respective correlations. Specifically, given information concerning the affinity among genes (i.e., connectivity in the gene regulatory network) and knowledge whether they promote/inhibit co-expression of the respective protein production, we seek rates that may explain the observed stationary distributions at the level of proteins. We propose to encapsulate their ``promotion vs.\ inhibition'' functionality in a sign-indefinite probability transition matrix--a matrix whose row-sums equal to one, but is otherwise sign indefinite. The purpose of constructing such a representation for the interaction network with sign-indefinite contributions in protein regulation, is to quantify the structure and significance of various links, and to explain how these may affect the geometry of the network, highlighting the significance of the regulatory functions of certain genes. We cast the problem of finding the interaction (sign-indefinite) transition matrix as a solution to a convex optimization problem from which all the relevant geometric properties may be easily derived.

Stochastic dynamical modeling of turbulent flows

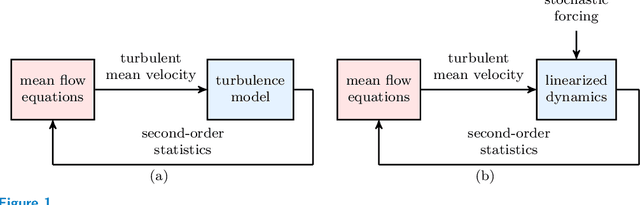
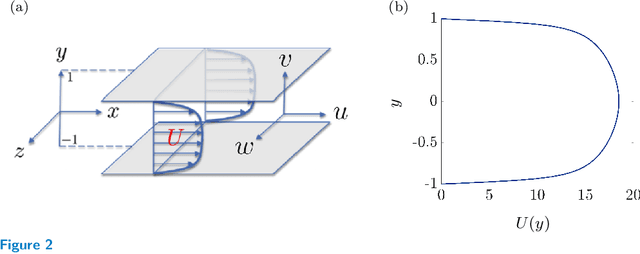
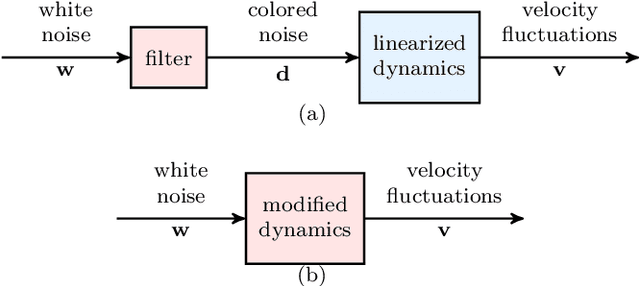
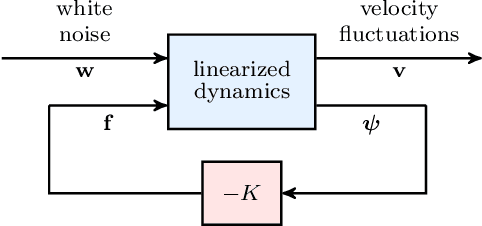
Advanced measurement techniques and high performance computing have made large data sets available for a wide range of turbulent flows that arise in engineering applications. Drawing on this abundance of data, dynamical models can be constructed to reproduce structural and statistical features of turbulent flows, opening the way to the design of effective model-based flow control strategies. This review describes a framework for completing second-order statistics of turbulent flows by models that are based on the Navier-Stokes equations linearized around the turbulent mean velocity. Systems theory and convex optimization are combined to address the inherent uncertainty in the dynamics and the statistics of the flow by seeking a suitable parsimonious correction to the prior linearized model. Specifically, dynamical couplings between states of the linearized model dictate structural constraints on the statistics of flow fluctuations. Thence, colored-in-time stochastic forcing that drives the linearized model is sought to account for and reconcile dynamics with available data (i.e., partially known second order statistics). The number of dynamical degrees of freedom that are directly affected by stochastic excitation is minimized as a measure of model parsimony. The spectral content of the resulting colored-in-time stochastic contribution can alternatively be seen to arise from a low-rank structural perturbation of the linearized dynamical generator, pointing to suitable dynamical corrections that may account for the absence of the nonlinear interactions in the linearized model.

Probabilistic Kernel Support Vector Machines

We propose a probabilistic enhancement of standard {\em kernel Support Vector Machines} for binary classification, in order to address the case when, along with given data sets, a description of uncertainty (e.g., error bounds) may be available on each datum. In the present paper, we specifically consider Gaussian distributions to model uncertainty. Thereby, our data consist of pairs $(x_i,\Sigma_i)$, $i\in\{1,\ldots,N\}$, along with an indicator $y_i\in\{-1,1\}$ to declare membership in one of two categories for each pair. These pairs may be viewed to represent the mean and covariance, respectively, of random vectors $\xi_i$ taking values in a suitable linear space (typically ${\mathbb R}^n$). Thus, our setting may also be viewed as a modification of Support Vector Machines to classify distributions, albeit, at present, only Gaussian ones. We outline the formalism that allows computing suitable classifiers via a natural modification of the standard ``kernel trick.'' The main contribution of this work is to point out a suitable kernel function for applying Support Vector techniques to the setting of uncertain data for which a detailed uncertainty description is also available (herein, ``Gaussian points'').

Proximal algorithms for large-scale statistical modeling and optimal sensor/actuator selection

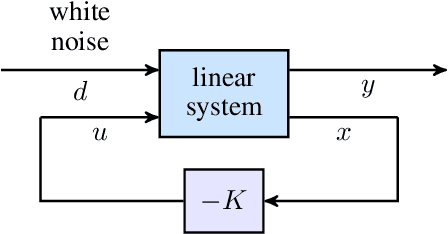
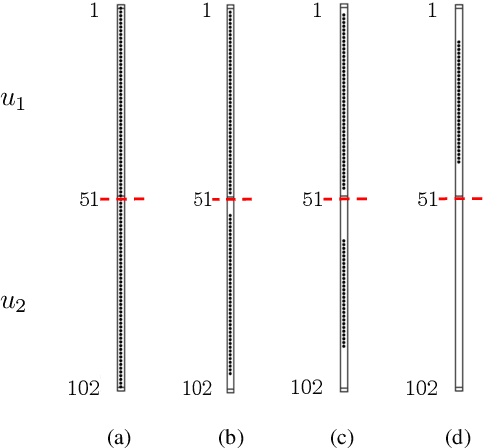
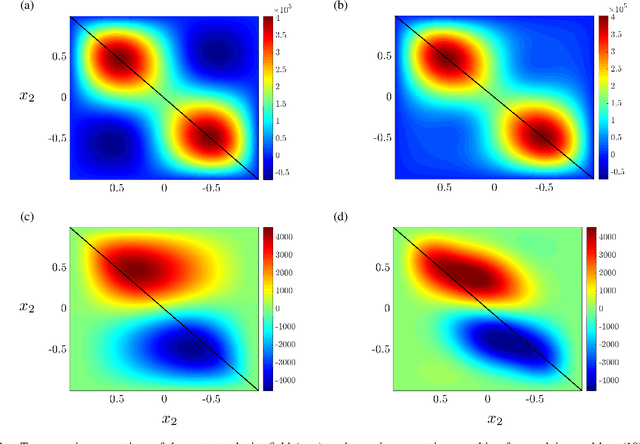
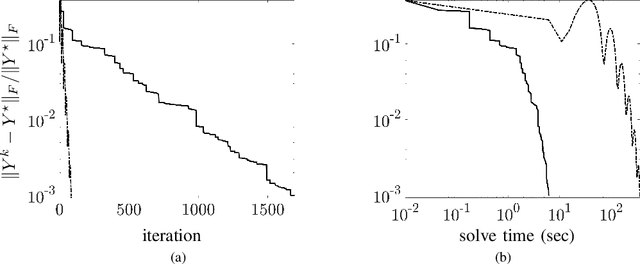
Several problems in modeling and control of stochastically-driven dynamical systems can be cast as regularized semi-definite programs. We examine two such representative problems and show that they can be formulated in a similar manner. The first, in statistical modeling, seeks to reconcile observed statistics by suitably and minimally perturbing prior dynamics. The second, seeks to optimally select sensors and actuators for control purposes. To address modeling and control of large-scale systems we develop a unified algorithmic framework using proximal methods. Our customized algorithms exploit problem structure and allow handling statistical modeling, as well as sensor and actuator selection, for substantially larger scales than what is amenable to current general-purpose solvers.