Proximal algorithms for large-scale statistical modeling and optimal sensor/actuator selection

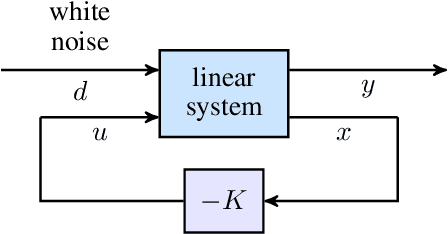
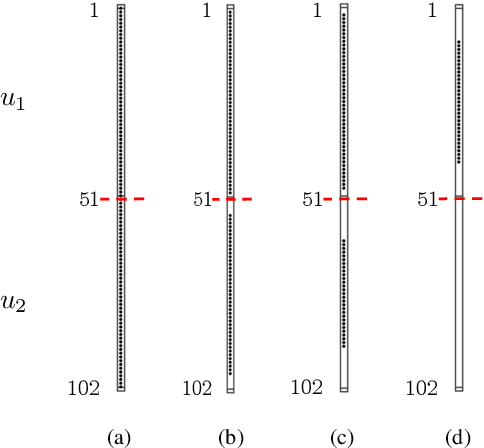
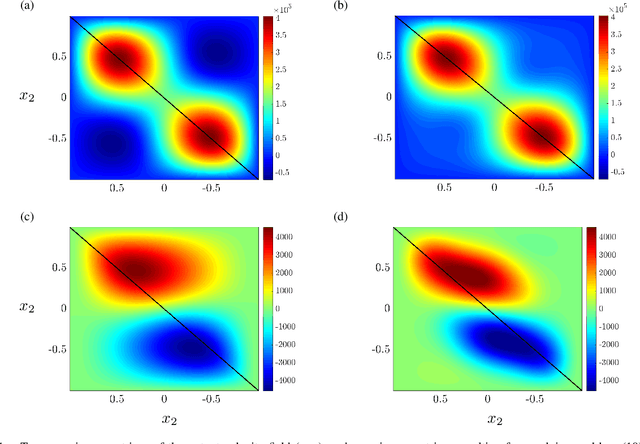
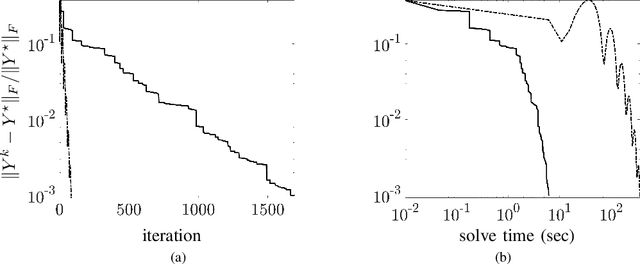
Several problems in modeling and control of stochastically-driven dynamical systems can be cast as regularized semi-definite programs. We examine two such representative problems and show that they can be formulated in a similar manner. The first, in statistical modeling, seeks to reconcile observed statistics by suitably and minimally perturbing prior dynamics. The second, seeks to optimally select sensors and actuators for control purposes. To address modeling and control of large-scale systems we develop a unified algorithmic framework using proximal methods. Our customized algorithms exploit problem structure and allow handling statistical modeling, as well as sensor and actuator selection, for substantially larger scales than what is amenable to current general-purpose solvers.