Optimal Transport for Kernel Gaussian Mixture Models

The Wasserstein distance from optimal mass transport (OMT) is a powerful mathematical tool with numerous applications that provides a natural measure of the distance between two probability distributions. Several methods to incorporate OMT into widely used probabilistic models, such as Gaussian or Gaussian mixture, have been developed to enhance the capability of modeling complex multimodal densities of real datasets. However, very few studies have explored the OMT problems in a reproducing kernel Hilbert space (RKHS), wherein the kernel trick is utilized to avoid the need to explicitly map input data into a high-dimensional feature space. In the current study, we propose a Wasserstein-type metric to compute the distance between two Gaussian mixtures in a RKHS via the kernel trick, i.e., kernel Gaussian mixture models.

Data Assimilation for Sign-indefinite Priors: A generalization of Sinkhorn's algorithm

The purpose of this work is to develop a framework to calibrate signed datasets so as to be consistent with specified marginals by suitably extending the Schr\"odinger-Fortet-Sinkhorn paradigm. Specifically, we seek to revise sign-indefinite multi-dimensional arrays in a way that the updated values agree with specified marginals. Our approach follows the rationale in Schr\"odinger's problem, aimed at updating a "prior" probability measure to agree with marginal distributions. The celebrated Sinkhorn's algorithm (established earlier by R.\ Fortet) that solves Schr\"odinger's problem found early applications in calibrating contingency tables in statistics and, more recently, multi-marginal problems in machine learning and optimal transport. Herein, we postulate a sign-indefinite prior in the form of a multi-dimensional array, and propose an optimization problem to suitably update this prior to ensure consistency with given marginals. The resulting algorithm generalizes the Sinkhorn algorithm in that it amounts to iterative scaling of the entries of the array along different coordinate directions. The scaling is multiplicative but also, in contrast to Sinkhorn, inverse-multiplicative depending on the sign of the entries. Our algorithm reduces to the classical Sinkhorn algorithm when the entries of the prior are positive.

Negative probabilities in Gene Regulatory Networks

We introduce a natural framework to identify sign-indefinite co-expressions between genes based on the known expressions and given the sign of their respective correlations. Specifically, given information concerning the affinity among genes (i.e., connectivity in the gene regulatory network) and knowledge whether they promote/inhibit co-expression of the respective protein production, we seek rates that may explain the observed stationary distributions at the level of proteins. We propose to encapsulate their ``promotion vs.\ inhibition'' functionality in a sign-indefinite probability transition matrix--a matrix whose row-sums equal to one, but is otherwise sign indefinite. The purpose of constructing such a representation for the interaction network with sign-indefinite contributions in protein regulation, is to quantify the structure and significance of various links, and to explain how these may affect the geometry of the network, highlighting the significance of the regulatory functions of certain genes. We cast the problem of finding the interaction (sign-indefinite) transition matrix as a solution to a convex optimization problem from which all the relevant geometric properties may be easily derived.

Wasserstein Image Local Analysis: Histogram of Orientations, Smoothing and Edge Detection

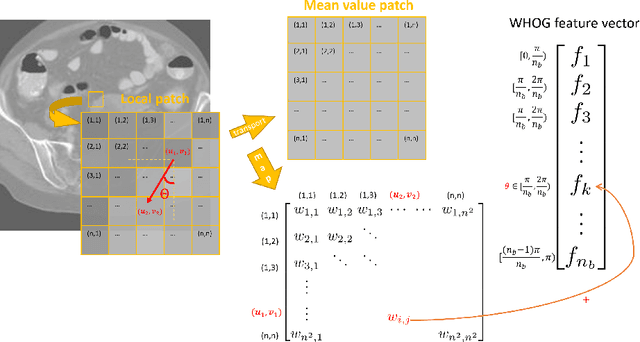
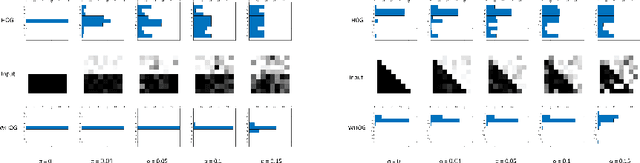
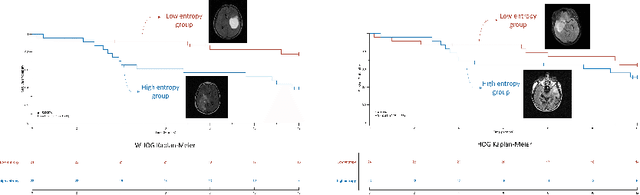
The Histogram of Oriented Gradient is a widely used image feature, which describes local image directionality based on numerical differentiation. Due to its ill-posed nature, small noise may lead to large errors. Conventional HOG may fail to produce meaningful directionality results in the presence of noise, which is common in medical radiographic imaging. We approach the directionality problem from a novel perspective by the use of the optimal transport map of a local image patch to a uni-color patch of its mean. We decompose the transport map into sub-work costs in different directions. We evaluated the ability of the optimal transport to quantify tumor heterogeneity from brain MRI images of patients with glioblastoma multiforme from the TCIA. By considering the entropy difference of the extracted local directionality within tumor regions, we found that patients with higher entropy in their images, had statistically significant worse overall survival (p $=0.008$), which indicates that tumors exhibiting flows in many directions may be more malignant, perhaps reflecting high tumor histologic grade, a reflection of histologic disorganization. We also explored the possibility of solving classical image processing problems such as smoothing and edge detection via optimal transport. By looking for a 2-color patch with minimum transport distance to a local patch, we derive a nonlinear shock filter, which preserves edges. Moreover, we found that the color difference of the computed 2-color patch indicates whether there is a large change in color, i.e., an edge in the given patch. In summary, we expand the usefulness of optimal transport as an image local analysis tool, to extract robust measures of imaging tumor heterogeneity for outcomes prediction as well as image pre-processing. Because of its robust nature, we find it offers several advantages over the classical approaches.

Optimal transport for vector Gaussian mixture models

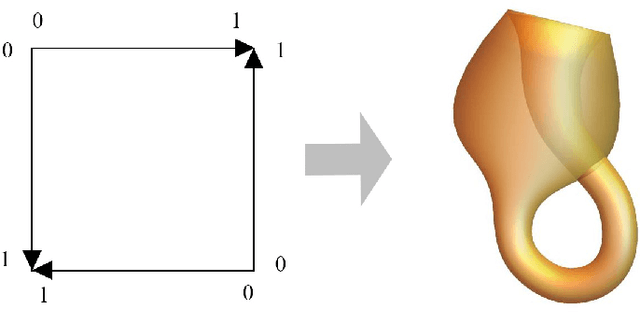
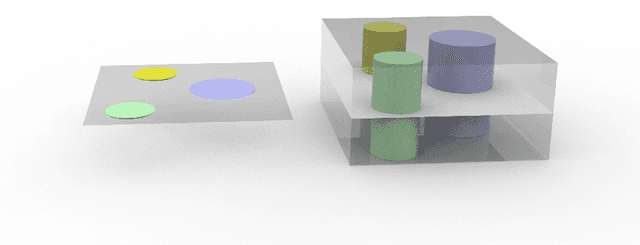
Vector Gaussian mixture models form an important special subset of vector-valued distributions. Any physical entity that can mutate or transit among alternative manifestations distributed in a given space falls into this category. A key example is color imagery. In this note, we vectorize the Gaussian mixture model and study different optimal mass transport related problems for such models. The benefits of using vector Gaussian mixture for optimal mass transport include computational efficiency and the ability to preserve structure.

Multimarginal Wasserstein Barycenter for Stain Normalization and Augmentation

Variations in hematoxylin and eosin (H&E) stained images (due to clinical lab protocols, scanners, etc) directly impact the quality and accuracy of clinical diagnosis, and hence it is important to control for these variations for a reliable diagnosis. In this work, we present a new approach based on the multimarginal Wasserstein barycenter to normalize and augment H&E stained images given one or more references. Specifically, we provide a mathematically robust way of naturally incorporating additional images as intermediate references to drive stain normalization and augmentation simultaneously. The presented approach showed superior results quantitatively and qualitatively as compared to state-of-the-art methods for stain normalization. We further validated our stain normalization and augmentations in the nuclei segmentation task on a publicly available dataset, achieving state-of-the-art results against competing approaches.

Kernel Wasserstein Distance

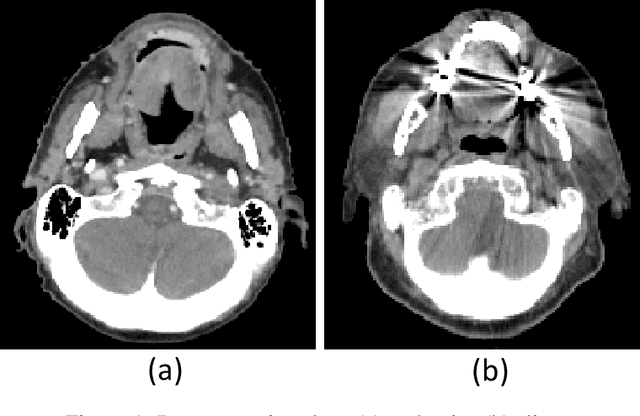
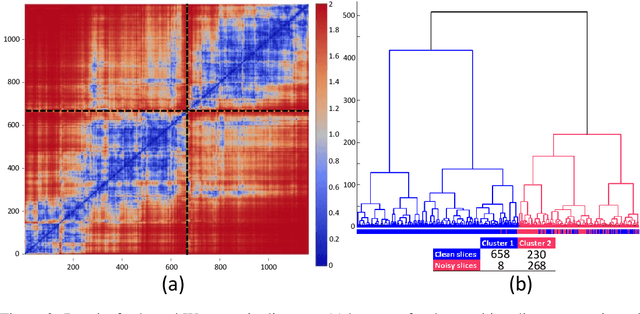
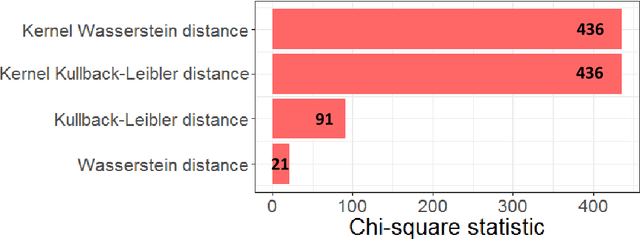
The Wasserstein distance is a powerful metric based on the theory of optimal transport. It gives a natural measure of the distance between two distributions with a wide range of applications. In contrast to a number of the common divergences on distributions such as Kullback-Leibler or Jensen-Shannon, it is (weakly) continuous, and thus ideal for analyzing corrupted data. To date, however, no kernel methods for dealing with nonlinear data have been proposed via the Wasserstein distance. In this work, we develop a novel method to compute the L2-Wasserstein distance in a kernel space implemented using the kernel trick. The latter is a general method in machine learning employed to handle data in a nonlinear manner. We evaluate the proposed approach in identifying computerized tomography (CT) slices with dental artifacts in head and neck cancer, performing unsupervised hierarchical clustering on the resulting Wasserstein distance matrix that is computed on imaging texture features extracted from each CT slice. Our experiments show that the kernel approach outperforms classical non-kernel approaches in identifying CT slices with artifacts.

Interpretable Spiculation Quantification for Lung Cancer Screening

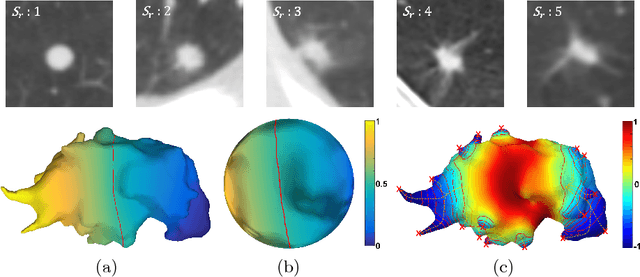
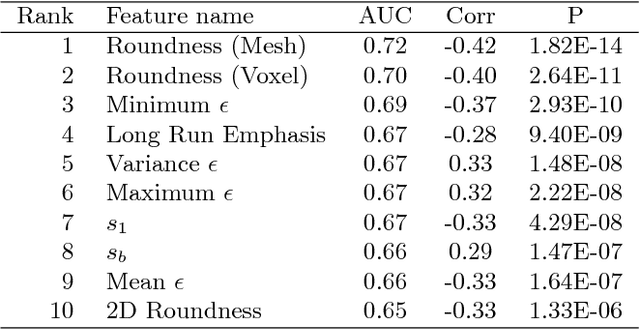
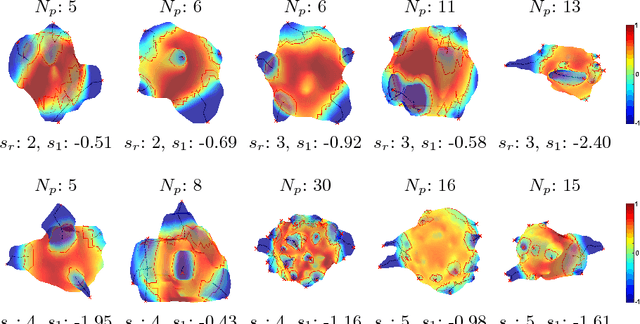
Spiculations are spikes on the surface of pulmonary nodule and are important predictors of malignancy in lung cancer. In this work, we introduced an interpretable, parameter-free technique for quantifying this critical feature using the area distortion metric from the spherical conformal (angle-preserving) parameterization. The conformal factor in the spherical mapping formulation provides a direct measure of spiculation which can be used to detect spikes and compute spike heights for geometrically-complex spiculations. The use of the area distortion metric from conformal mapping has never been exploited before in this context. Based on the area distortion metric and the spiculation height, we introduced a novel spiculation score. A combination of our spiculation measures was found to be highly correlated (Spearman's rank correlation coefficient $\rho = 0.48$) with the radiologist's spiculation score. These measures were also used in the radiomics framework to achieve state-of-the-art malignancy prediction accuracy of 88.9% on a publicly available dataset.

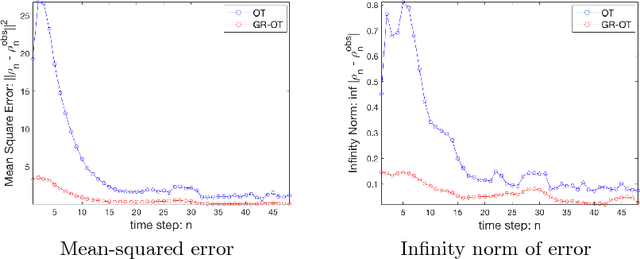
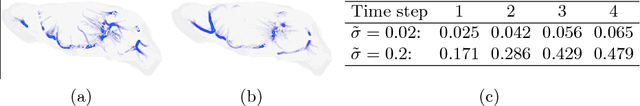
GlymphVIS: Visualizing Glymphatic Transport Pathways Using Regularized Optimal Transport

The glymphatic system (GS) is a transit passage that facilitates brain metabolic waste removal and its dysfunction has been associated with neurodegenerative diseases such as Alzheimer's disease. The GS has been studied by acquiring temporal contrast enhanced magnetic resonance imaging (MRI) sequences of a rodent brain, and tracking the cerebrospinal fluid injected contrast agent as it flows through the GS. We present here a novel visualization framework, GlymphVIS, which uses regularized optimal transport (OT) to study the flow behavior between time points at which the images are taken. Using this regularized OT approach, we can incorporate diffusion, handle noise, and accurately capture and visualize the time varying dynamics in GS transport. Moreover, we are able to reduce the registration mean-squared and infinity-norm error across time points by up to a factor of 5 as compared to the current state-of-the-art method. Our visualization pipeline yields flow patterns that align well with experts' current findings of the glymphatic system.

Affine Differential Invariants for Invariant Feature Point Detection

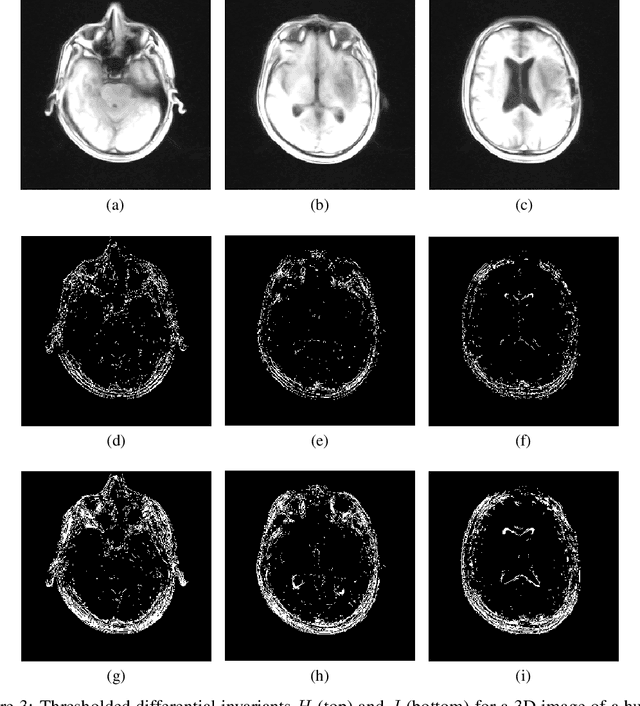
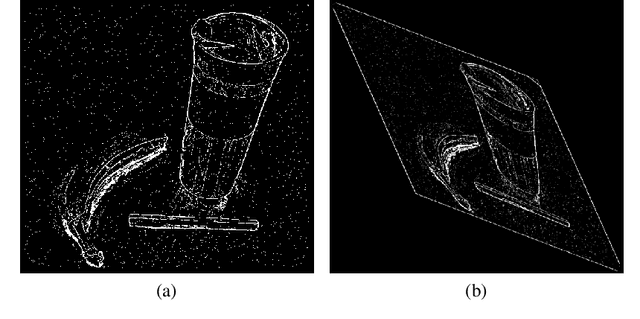
Image feature points are detected as pixels which locally maximize a detector function, two commonly used examples of which are the (Euclidean) image gradient and the Harris-Stephens corner detector. A major limitation of these feature detectors are that they are only Euclidean-invariant. In this work we demonstrate the application of a 2D affine-invariant image feature point detector based on differential invariants as derived through the equivariant method of moving frames. The fundamental equi-affine differential invariants for 3D image volumes are also computed.