Rena Elkin
Optimal Transport for Kernel Gaussian Mixture Models
Oct 28, 2023Abstract:The Wasserstein distance from optimal mass transport (OMT) is a powerful mathematical tool with numerous applications that provides a natural measure of the distance between two probability distributions. Several methods to incorporate OMT into widely used probabilistic models, such as Gaussian or Gaussian mixture, have been developed to enhance the capability of modeling complex multimodal densities of real datasets. However, very few studies have explored the OMT problems in a reproducing kernel Hilbert space (RKHS), wherein the kernel trick is utilized to avoid the need to explicitly map input data into a high-dimensional feature space. In the current study, we propose a Wasserstein-type metric to compute the distance between two Gaussian mixtures in a RKHS via the kernel trick, i.e., kernel Gaussian mixture models.
GlymphVIS: Visualizing Glymphatic Transport Pathways Using Regularized Optimal Transport
Sep 01, 2018
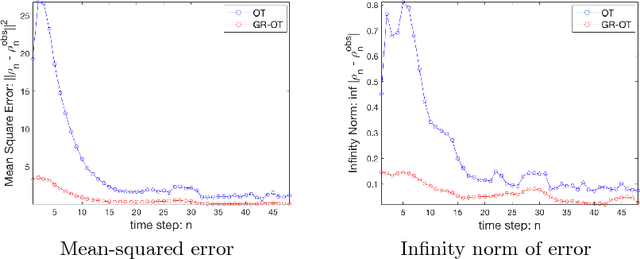
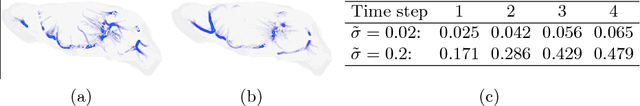

Abstract:The glymphatic system (GS) is a transit passage that facilitates brain metabolic waste removal and its dysfunction has been associated with neurodegenerative diseases such as Alzheimer's disease. The GS has been studied by acquiring temporal contrast enhanced magnetic resonance imaging (MRI) sequences of a rodent brain, and tracking the cerebrospinal fluid injected contrast agent as it flows through the GS. We present here a novel visualization framework, GlymphVIS, which uses regularized optimal transport (OT) to study the flow behavior between time points at which the images are taken. Using this regularized OT approach, we can incorporate diffusion, handle noise, and accurately capture and visualize the time varying dynamics in GS transport. Moreover, we are able to reduce the registration mean-squared and infinity-norm error across time points by up to a factor of 5 as compared to the current state-of-the-art method. Our visualization pipeline yields flow patterns that align well with experts' current findings of the glymphatic system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge