Optimal Transport for Kernel Gaussian Mixture Models

The Wasserstein distance from optimal mass transport (OMT) is a powerful mathematical tool with numerous applications that provides a natural measure of the distance between two probability distributions. Several methods to incorporate OMT into widely used probabilistic models, such as Gaussian or Gaussian mixture, have been developed to enhance the capability of modeling complex multimodal densities of real datasets. However, very few studies have explored the OMT problems in a reproducing kernel Hilbert space (RKHS), wherein the kernel trick is utilized to avoid the need to explicitly map input data into a high-dimensional feature space. In the current study, we propose a Wasserstein-type metric to compute the distance between two Gaussian mixtures in a RKHS via the kernel trick, i.e., kernel Gaussian mixture models.

Wasserstein Image Local Analysis: Histogram of Orientations, Smoothing and Edge Detection

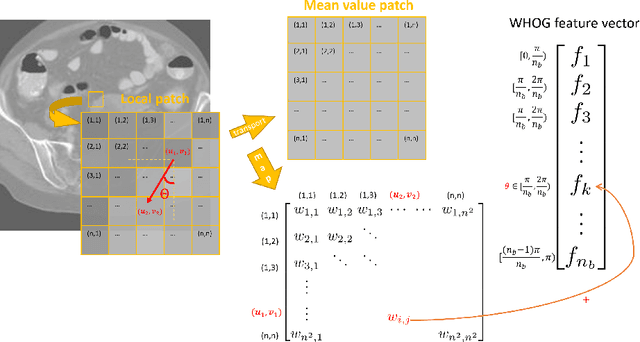
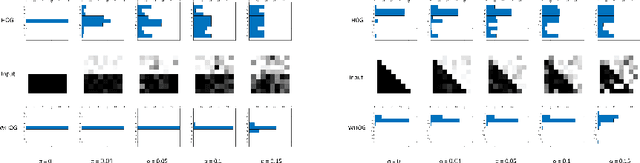
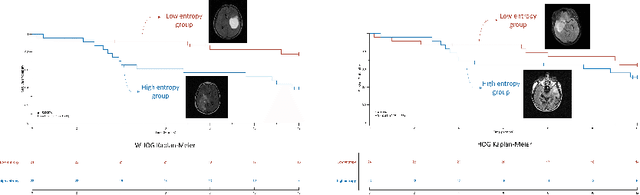
The Histogram of Oriented Gradient is a widely used image feature, which describes local image directionality based on numerical differentiation. Due to its ill-posed nature, small noise may lead to large errors. Conventional HOG may fail to produce meaningful directionality results in the presence of noise, which is common in medical radiographic imaging. We approach the directionality problem from a novel perspective by the use of the optimal transport map of a local image patch to a uni-color patch of its mean. We decompose the transport map into sub-work costs in different directions. We evaluated the ability of the optimal transport to quantify tumor heterogeneity from brain MRI images of patients with glioblastoma multiforme from the TCIA. By considering the entropy difference of the extracted local directionality within tumor regions, we found that patients with higher entropy in their images, had statistically significant worse overall survival (p $=0.008$), which indicates that tumors exhibiting flows in many directions may be more malignant, perhaps reflecting high tumor histologic grade, a reflection of histologic disorganization. We also explored the possibility of solving classical image processing problems such as smoothing and edge detection via optimal transport. By looking for a 2-color patch with minimum transport distance to a local patch, we derive a nonlinear shock filter, which preserves edges. Moreover, we found that the color difference of the computed 2-color patch indicates whether there is a large change in color, i.e., an edge in the given patch. In summary, we expand the usefulness of optimal transport as an image local analysis tool, to extract robust measures of imaging tumor heterogeneity for outcomes prediction as well as image pre-processing. Because of its robust nature, we find it offers several advantages over the classical approaches.

Optimal transport for vector Gaussian mixture models

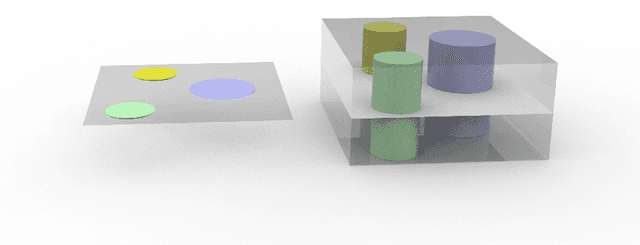
Vector Gaussian mixture models form an important special subset of vector-valued distributions. Any physical entity that can mutate or transit among alternative manifestations distributed in a given space falls into this category. A key example is color imagery. In this note, we vectorize the Gaussian mixture model and study different optimal mass transport related problems for such models. The benefits of using vector Gaussian mixture for optimal mass transport include computational efficiency and the ability to preserve structure.