Optimal Transport for Kernel Gaussian Mixture Models

The Wasserstein distance from optimal mass transport (OMT) is a powerful mathematical tool with numerous applications that provides a natural measure of the distance between two probability distributions. Several methods to incorporate OMT into widely used probabilistic models, such as Gaussian or Gaussian mixture, have been developed to enhance the capability of modeling complex multimodal densities of real datasets. However, very few studies have explored the OMT problems in a reproducing kernel Hilbert space (RKHS), wherein the kernel trick is utilized to avoid the need to explicitly map input data into a high-dimensional feature space. In the current study, we propose a Wasserstein-type metric to compute the distance between two Gaussian mixtures in a RKHS via the kernel trick, i.e., kernel Gaussian mixture models.

Kernel Wasserstein Distance

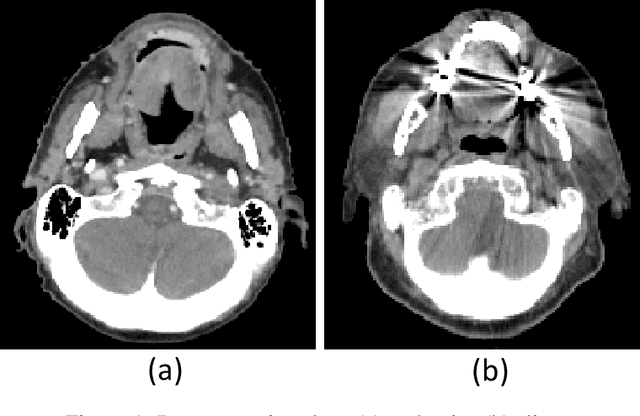
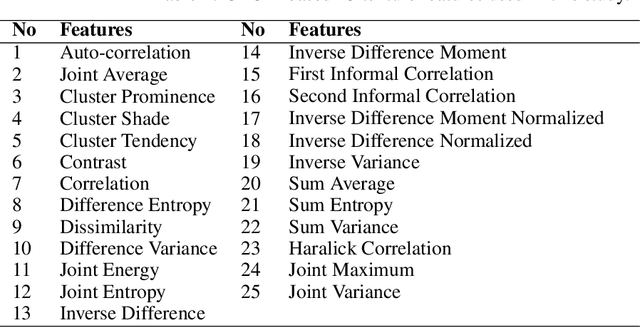
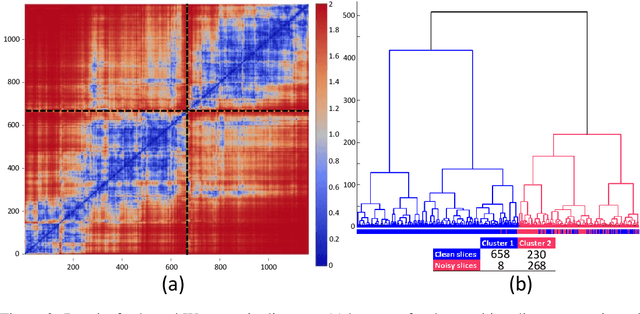
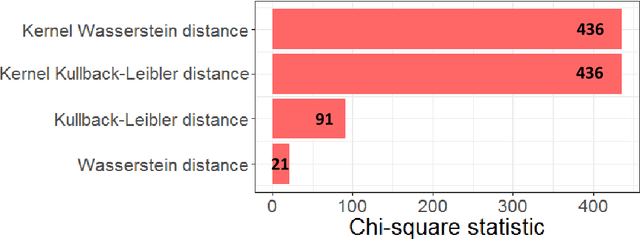
The Wasserstein distance is a powerful metric based on the theory of optimal transport. It gives a natural measure of the distance between two distributions with a wide range of applications. In contrast to a number of the common divergences on distributions such as Kullback-Leibler or Jensen-Shannon, it is (weakly) continuous, and thus ideal for analyzing corrupted data. To date, however, no kernel methods for dealing with nonlinear data have been proposed via the Wasserstein distance. In this work, we develop a novel method to compute the L2-Wasserstein distance in a kernel space implemented using the kernel trick. The latter is a general method in machine learning employed to handle data in a nonlinear manner. We evaluate the proposed approach in identifying computerized tomography (CT) slices with dental artifacts in head and neck cancer, performing unsupervised hierarchical clustering on the resulting Wasserstein distance matrix that is computed on imaging texture features extracted from each CT slice. Our experiments show that the kernel approach outperforms classical non-kernel approaches in identifying CT slices with artifacts.