Hyperphantasia: A Benchmark for Evaluating the Mental Visualization Capabilities of Multimodal LLMs

Mental visualization, the ability to construct and manipulate visual representations internally, is a core component of human cognition and plays a vital role in tasks involving reasoning, prediction, and abstraction. Despite the rapid progress of Multimodal Large Language Models (MLLMs), current benchmarks primarily assess passive visual perception, offering limited insight into the more active capability of internally constructing visual patterns to support problem solving. Yet mental visualization is a critical cognitive skill in humans, supporting abilities such as spatial navigation, predicting physical trajectories, and solving complex visual problems through imaginative simulation. To bridge this gap, we introduce Hyperphantasia, a synthetic benchmark designed to evaluate the mental visualization abilities of MLLMs through four carefully constructed puzzles. Each task is procedurally generated and presented at three difficulty levels, enabling controlled analysis of model performance across increasing complexity. Our comprehensive evaluation of state-of-the-art models reveals a substantial gap between the performance of humans and MLLMs. Additionally, we explore the potential of reinforcement learning to improve visual simulation capabilities. Our findings suggest that while some models exhibit partial competence in recognizing visual patterns, robust mental visualization remains an open challenge for current MLLMs.

Emergence and Evolution of Interpretable Concepts in Diffusion Models

Diffusion models have become the go-to method for text-to-image generation, producing high-quality images from noise through a process called reverse diffusion. Understanding the dynamics of the reverse diffusion process is crucial in steering the generation and achieving high sample quality. However, the inner workings of diffusion models is still largely a mystery due to their black-box nature and complex, multi-step generation process. Mechanistic Interpretability (MI) techniques, such as Sparse Autoencoders (SAEs), aim at uncovering the operating principles of models through granular analysis of their internal representations. These MI techniques have been successful in understanding and steering the behavior of large language models at scale. However, the great potential of SAEs has not yet been applied toward gaining insight into the intricate generative process of diffusion models. In this work, we leverage the SAE framework to probe the inner workings of a popular text-to-image diffusion model, and uncover a variety of human-interpretable concepts in its activations. Interestingly, we find that even before the first reverse diffusion step is completed, the final composition of the scene can be predicted surprisingly well by looking at the spatial distribution of activated concepts. Moreover, going beyond correlational analysis, we show that the discovered concepts have a causal effect on the model output and can be leveraged to steer the generative process. We design intervention techniques aimed at manipulating image composition and style, and demonstrate that (1) in early stages of diffusion image composition can be effectively controlled, (2) in the middle stages of diffusion image composition is finalized, however stylistic interventions are effective, and (3) in the final stages of diffusion only minor textural details are subject to change.

Adapt and Diffuse: Sample-adaptive Reconstruction via Latent Diffusion Models

Inverse problems arise in a multitude of applications, where the goal is to recover a clean signal from noisy and possibly (non)linear observations. The difficulty of a reconstruction problem depends on multiple factors, such as the structure of the ground truth signal, the severity of the degradation, the implicit bias of the reconstruction model and the complex interactions between the above factors. This results in natural sample-by-sample variation in the difficulty of a reconstruction task, which is often overlooked by contemporary techniques. Recently, diffusion-based inverse problem solvers have established new state-of-the-art in various reconstruction tasks. However, they have the drawback of being computationally prohibitive. Our key observation in this paper is that most existing solvers lack the ability to adapt their compute power to the difficulty of the reconstruction task, resulting in long inference times, subpar performance and wasteful resource allocation. We propose a novel method that we call severity encoding, to estimate the degradation severity of noisy, degraded signals in the latent space of an autoencoder. We show that the estimated severity has strong correlation with the true corruption level and can give useful hints at the difficulty of reconstruction problems on a sample-by-sample basis. Furthermore, we propose a reconstruction method based on latent diffusion models that leverages the predicted degradation severities to fine-tune the reverse diffusion sampling trajectory and thus achieve sample-adaptive inference times. We utilize latent diffusion posterior sampling to maintain data consistency with observations. We perform experiments on both linear and nonlinear inverse problems and demonstrate that our technique achieves performance comparable to state-of-the-art diffusion-based techniques, with significant improvements in computational efficiency.

DiracDiffusion: Denoising and Incremental Reconstruction with Assured Data-Consistency

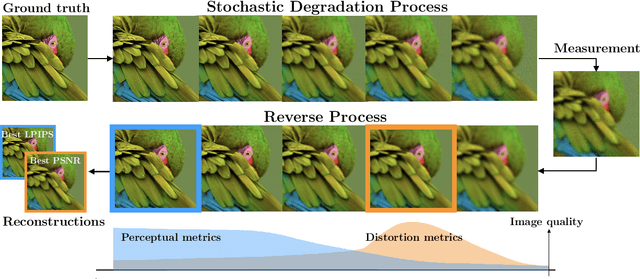
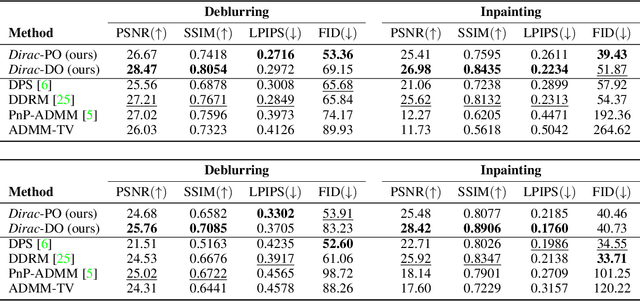
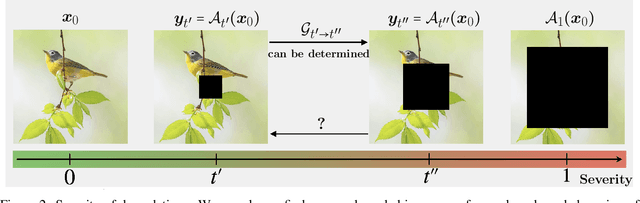
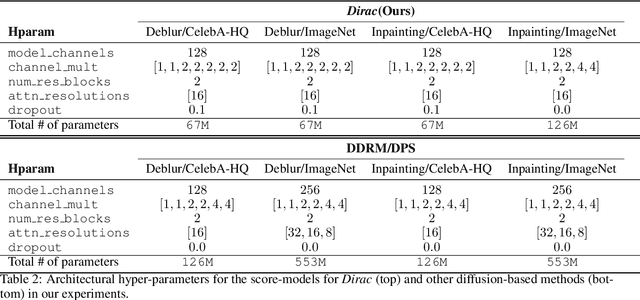
Diffusion models have established new state of the art in a multitude of computer vision tasks, including image restoration. Diffusion-based inverse problem solvers generate reconstructions of exceptional visual quality from heavily corrupted measurements. However, in what is widely known as the perception-distortion trade-off, the price of perceptually appealing reconstructions is often paid in declined distortion metrics, such as PSNR. Distortion metrics measure faithfulness to the observation, a crucial requirement in inverse problems. In this work, we propose a novel framework for inverse problem solving, namely we assume that the observation comes from a stochastic degradation process that gradually degrades and noises the original clean image. We learn to reverse the degradation process in order to recover the clean image. Our technique maintains consistency with the original measurement throughout the reverse process, and allows for great flexibility in trading off perceptual quality for improved distortion metrics and sampling speedup via early-stopping. We demonstrate the efficiency of our method on different high-resolution datasets and inverse problems, achieving great improvements over other state-of-the-art diffusion-based methods with respect to both perceptual and distortion metrics. Source code and pre-trained models will be released soon.