DiracDiffusion: Denoising and Incremental Reconstruction with Assured Data-Consistency
Paper and Code
Mar 25, 2023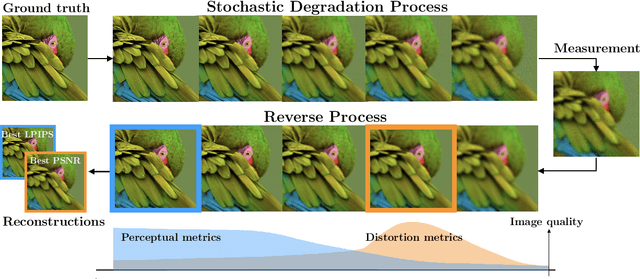
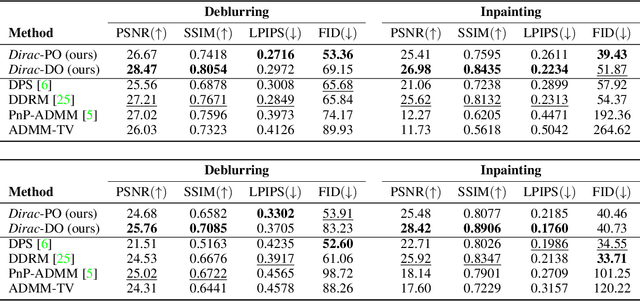
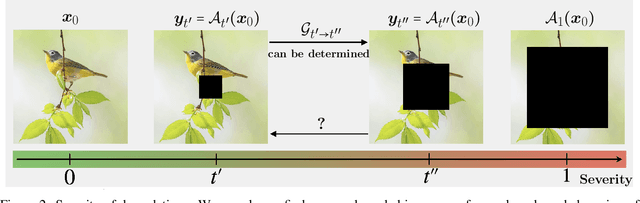
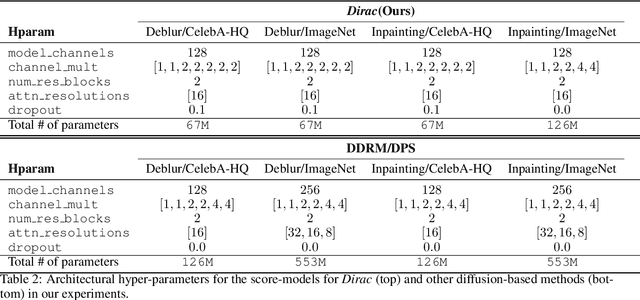
Diffusion models have established new state of the art in a multitude of computer vision tasks, including image restoration. Diffusion-based inverse problem solvers generate reconstructions of exceptional visual quality from heavily corrupted measurements. However, in what is widely known as the perception-distortion trade-off, the price of perceptually appealing reconstructions is often paid in declined distortion metrics, such as PSNR. Distortion metrics measure faithfulness to the observation, a crucial requirement in inverse problems. In this work, we propose a novel framework for inverse problem solving, namely we assume that the observation comes from a stochastic degradation process that gradually degrades and noises the original clean image. We learn to reverse the degradation process in order to recover the clean image. Our technique maintains consistency with the original measurement throughout the reverse process, and allows for great flexibility in trading off perceptual quality for improved distortion metrics and sampling speedup via early-stopping. We demonstrate the efficiency of our method on different high-resolution datasets and inverse problems, achieving great improvements over other state-of-the-art diffusion-based methods with respect to both perceptual and distortion metrics. Source code and pre-trained models will be released soon.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge