OMAC: A Broad Optimization Framework for LLM-Based Multi-Agent Collaboration

Agents powered by advanced large language models (LLMs) have demonstrated impressive capabilities across diverse complex applications. Recently, Multi-Agent Systems (MAS), wherein multiple agents collaborate and communicate with each other, have exhibited enhanced capabilities in complex tasks, such as high-quality code generation and arithmetic reasoning. However, the development of such systems often relies on handcrafted methods, and the literature on systematic design and optimization of LLM-based MAS remains limited. In this work, we introduce OMAC, a general framework designed for holistic optimization of LLM-based MAS. Specifically, we identify five key optimization dimensions for MAS, encompassing both agent functionality and collaboration structure. Building upon these dimensions, we first propose a general algorithm, utilizing two actors termed the Semantic Initializer and the Contrastive Comparator, to optimize any single dimension. Then, we present an algorithm for joint optimization across multiple dimensions. Extensive experiments demonstrate the superior performance of OMAC on code generation, arithmetic reasoning, and general reasoning tasks against state-of-the-art approaches.

Goal-Conditioned Supervised Learning for Multi-Objective Recommendation

Multi-objective learning endeavors to concurrently optimize multiple objectives using a single model, aiming to achieve high and balanced performance across these diverse objectives. However, it often involves a more complex optimization problem, particularly when navigating potential conflicts between objectives, leading to solutions with higher memory requirements and computational complexity. This paper introduces a Multi-Objective Goal-Conditioned Supervised Learning (MOGCSL) framework for automatically learning to achieve multiple objectives from offline sequential data. MOGCSL extends the conventional Goal-Conditioned Supervised Learning (GCSL) method to multi-objective scenarios by redefining goals from one-dimensional scalars to multi-dimensional vectors. The need for complex architectures and optimization constraints can be naturally eliminated. MOGCSL benefits from filtering out uninformative or noisy instances that do not achieve desirable long-term rewards. It also incorporates a novel goal-choosing algorithm to model and select "high" achievable goals for inference. While MOGCSL is quite general, we focus on its application to the next action prediction problem in commercial-grade recommender systems. In this context, any viable solution needs to be reasonably scalable and also be robust to large amounts of noisy data that is characteristic of this application space. We show that MOGCSL performs admirably on both counts. Specifically, extensive experiments conducted on real-world recommendation datasets validate its efficacy and efficiency. Also, analysis and experiments are included to explain its strength in discounting the noisier portions of training data in recommender systems.

HyQE: Ranking Contexts with Hypothetical Query Embeddings

In retrieval-augmented systems, context ranking techniques are commonly employed to reorder the retrieved contexts based on their relevance to a user query. A standard approach is to measure this relevance through the similarity between contexts and queries in the embedding space. However, such similarity often fails to capture the relevance. Alternatively, large language models (LLMs) have been used for ranking contexts. However, they can encounter scalability issues when the number of candidate contexts grows and the context window sizes of the LLMs remain constrained. Additionally, these approaches require fine-tuning LLMs with domain-specific data. In this work, we introduce a scalable ranking framework that combines embedding similarity and LLM capabilities without requiring LLM fine-tuning. Our framework uses a pre-trained LLM to hypothesize the user query based on the retrieved contexts and ranks the context based on the similarity between the hypothesized queries and the user query. Our framework is efficient at inference time and is compatible with many other retrieval and ranking techniques. Experimental results show that our method improves the ranking performance across multiple benchmarks. The complete code and data are available at https://github.com/zwc662/hyqe

Theoretical Guarantees of Learning Ensembling Strategies with Applications to Time Series Forecasting

Ensembling is among the most popular tools in machine learning (ML) due to its effectiveness in minimizing variance and thus improving generalization. Most ensembling methods for black-box base learners fall under the umbrella of "stacked generalization," namely training an ML algorithm that takes the inferences from the base learners as input. While stacking has been widely applied in practice, its theoretical properties are poorly understood. In this paper, we prove a novel result, showing that choosing the best stacked generalization from a (finite or finite-dimensional) family of stacked generalizations based on cross-validated performance does not perform "much worse" than the oracle best. Our result strengthens and significantly extends the results in Van der Laan et al. (2007). Inspired by the theoretical analysis, we further propose a particular family of stacked generalizations in the context of probabilistic forecasting, each one with a different sensitivity for how much the ensemble weights are allowed to vary across items, timestamps in the forecast horizon, and quantiles. Experimental results demonstrate the performance gain of the proposed method.

Testing Causality for High Dimensional Data

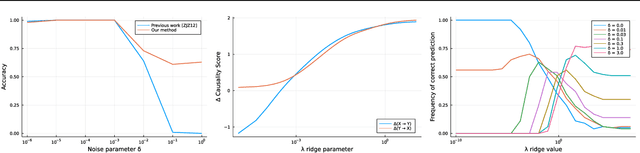
Determining causal relationship between high dimensional observations are among the most important tasks in scientific discoveries. In this paper, we revisited the \emph{linear trace method}, a technique proposed in~\citep{janzing2009telling,zscheischler2011testing} to infer the causal direction between two random variables of high dimensions. We strengthen the existing results significantly by providing an improved tail analysis in addition to extending the results to nonlinear trace functionals with sharper confidence bounds under certain distributional assumptions. We obtain our results by interpreting the trace estimator in the causal regime as a function over random orthogonal matrices, where the concentration of Lipschitz functions over such space could be applied. We additionally propose a novel ridge-regularized variant of the estimator in \cite{zscheischler2011testing}, and give provable bounds relating the ridge-estimated terms to their ground-truth counterparts. We support our theoretical results with encouraging experiments on synthetic datasets, more prominently, under high-dimension low sample size regime.

Towards Robust Multivariate Time-Series Forecasting: Adversarial Attacks and Defense Mechanisms

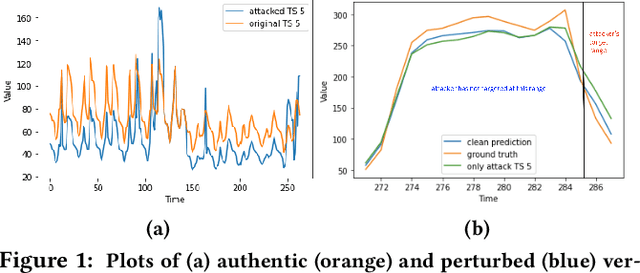
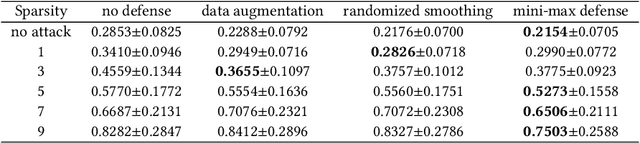
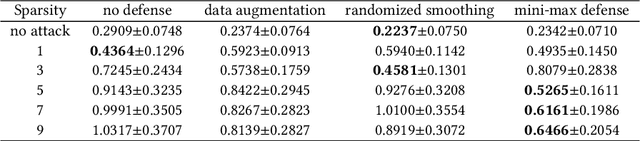
As deep learning models have gradually become the main workhorse of time series forecasting, the potential vulnerability under adversarial attacks to forecasting and decision system accordingly has emerged as a main issue in recent years. Albeit such behaviors and defense mechanisms started to be investigated for the univariate time series forecasting, there are still few studies regarding the multivariate forecasting which is often preferred due to its capacity to encode correlations between different time series. In this work, we study and design adversarial attack on multivariate probabilistic forecasting models, taking into consideration attack budget constraints and the correlation architecture between multiple time series. Specifically, we investigate a sparse indirect attack that hurts the prediction of an item (time series) by only attacking the history of a small number of other items to save attacking cost. In order to combat these attacks, we also develop two defense strategies. First, we adopt randomized smoothing to multivariate time series scenario and verify its effectiveness via empirical experiments. Second, we leverage a sparse attacker to enable end-to-end adversarial training that delivers robust probabilistic forecasters. Extensive experiments on real dataset confirm that our attack schemes are powerful and our defend algorithms are more effective compared with other baseline defense mechanisms.

Dynamic Regret for Strongly Adaptive Methods and Optimality of Online KRR

We consider the framework of non-stationary Online Convex Optimization where a learner seeks to control its dynamic regret against an arbitrary sequence of comparators. When the loss functions are strongly convex or exp-concave, we demonstrate that Strongly Adaptive (SA) algorithms can be viewed as a principled way of controlling dynamic regret in terms of path variation $V_T$ of the comparator sequence. Specifically, we show that SA algorithms enjoy $\tilde O(\sqrt{TV_T} \vee \log T)$ and $\tilde O(\sqrt{dTV_T} \vee d\log T)$ dynamic regret for strongly convex and exp-concave losses respectively without apriori knowledge of $V_T$. The versatility of the principled approach is further demonstrated by the novel results in the setting of learning against bounded linear predictors and online regression with Gaussian kernels. Under a related setting, the second component of the paper addresses an open question posed by Zhdanov and Kalnishkan (2010) that concerns online kernel regression with squared error losses. We derive a new lower bound on a certain penalized regret which establishes the near minimax optimality of online Kernel Ridge Regression (KRR). Our lower bound can be viewed as an RKHS extension to the lower bound derived in Vovk (2001) for online linear regression in finite dimensions.