Regression with Cost-based Rejection

Learning with rejection is an important framework that can refrain from making predictions to avoid critical mispredictions by balancing between prediction and rejection. Previous studies on cost-based rejection only focused on the classification setting, which cannot handle the continuous and infinite target space in the regression setting. In this paper, we investigate a novel regression problem called regression with cost-based rejection, where the model can reject to make predictions on some examples given certain rejection costs. To solve this problem, we first formulate the expected risk for this problem and then derive the Bayes optimal solution, which shows that the optimal model should reject to make predictions on the examples whose variance is larger than the rejection cost when the mean squared error is used as the evaluation metric. Furthermore, we propose to train the model by a surrogate loss function that considers rejection as binary classification and we provide conditions for the model consistency, which implies that the Bayes optimal solution can be recovered by our proposed surrogate loss. Extensive experiments demonstrate the effectiveness of our proposed method.

In Defense of Softmax Parametrization for Calibrated and Consistent Learning to Defer

Enabling machine learning classifiers to defer their decision to a downstream expert when the expert is more accurate will ensure improved safety and performance. This objective can be achieved with the learning-to-defer framework which aims to jointly learn how to classify and how to defer to the expert. In recent studies, it has been theoretically shown that popular estimators for learning to defer parameterized with softmax provide unbounded estimates for the likelihood of deferring which makes them uncalibrated. However, it remains unknown whether this is due to the widely used softmax parameterization and if we can find a softmax-based estimator that is both statistically consistent and possesses a valid probability estimator. In this work, we first show that the cause of the miscalibrated and unbounded estimator in prior literature is due to the symmetric nature of the surrogate losses used and not due to softmax. We then propose a novel statistically consistent asymmetric softmax-based surrogate loss that can produce valid estimates without the issue of unboundedness. We further analyze the non-asymptotic properties of our method and empirically validate its performance and calibration on benchmark datasets.

Weakly Supervised Regression with Interval Targets

This paper investigates an interesting weakly supervised regression setting called regression with interval targets (RIT). Although some of the previous methods on relevant regression settings can be adapted to RIT, they are not statistically consistent, and thus their empirical performance is not guaranteed. In this paper, we provide a thorough study on RIT. First, we proposed a novel statistical model to describe the data generation process for RIT and demonstrate its validity. Second, we analyze a simple selection method for RIT, which selects a particular value in the interval as the target value to train the model. Third, we propose a statistically consistent limiting method for RIT to train the model by limiting the predictions to the interval. We further derive an estimation error bound for our limiting method. Finally, extensive experiments on various datasets demonstrate the effectiveness of our proposed method.

On the Importance of Feature Separability in Predicting Out-Of-Distribution Error

Estimating the generalization performance is practically challenging on out-of-distribution (OOD) data without ground truth labels. While previous methods emphasize the connection between distribution difference and OOD accuracy, we show that a large domain gap not necessarily leads to a low test accuracy. In this paper, we investigate this problem from the perspective of feature separability, and propose a dataset-level score based upon feature dispersion to estimate the test accuracy under distribution shift. Our method is inspired by desirable properties of features in representation learning: high inter-class dispersion and high intra-class compactness. Our analysis shows that inter-class dispersion is strongly correlated with the model accuracy, while intra-class compactness does not reflect the generalization performance on OOD data. Extensive experiments demonstrate the superiority of our method in both prediction performance and computational efficiency.

Multi-Class Classification from Single-Class Data with Confidences

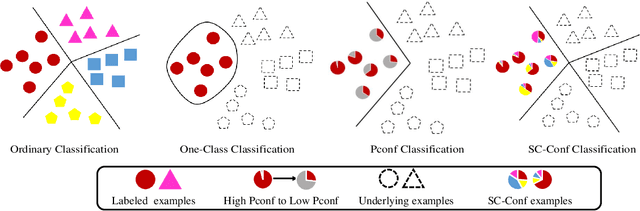
Can we learn a multi-class classifier from only data of a single class? We show that without any assumptions on the loss functions, models, and optimizers, we can successfully learn a multi-class classifier from only data of a single class with a rigorous consistency guarantee when confidences (i.e., the class-posterior probabilities for all the classes) are available. Specifically, we propose an empirical risk minimization framework that is loss-/model-/optimizer-independent. Instead of constructing a boundary between the given class and other classes, our method can conduct discriminative classification between all the classes even if no data from the other classes are provided. We further theoretically and experimentally show that our method can be Bayes-consistent with a simple modification even if the provided confidences are highly noisy. Then, we provide an extension of our method for the case where data from a subset of all the classes are available. Experimental results demonstrate the effectiveness of our methods.

Learning from Similarity-Confidence Data

Weakly supervised learning has drawn considerable attention recently to reduce the expensive time and labor consumption of labeling massive data. In this paper, we investigate a novel weakly supervised learning problem of learning from similarity-confidence (Sconf) data, where we aim to learn an effective binary classifier from only unlabeled data pairs equipped with confidence that illustrates their degree of similarity (two examples are similar if they belong to the same class). To solve this problem, we propose an unbiased estimator of the classification risk that can be calculated from only Sconf data and show that the estimation error bound achieves the optimal convergence rate. To alleviate potential overfitting when flexible models are used, we further employ a risk correction scheme on the proposed risk estimator. Experimental results demonstrate the effectiveness of the proposed methods.

Multi-Complementary and Unlabeled Learning for Arbitrary Losses and Models

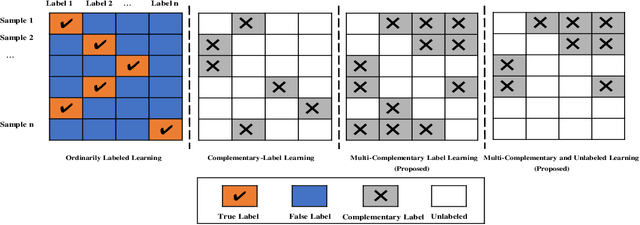
A weakly-supervised learning framework named as complementary-label learning has been proposed recently, where each sample is equipped with a single complementary label that denotes one of the classes the sample does not belong to. However, the existing complementary-label learning methods cannot learn from the easily accessible unlabeled samples and samples with multiple complementary labels, which are more informative. In this paper, to remove these limitations, we propose the novel multi-complementary and unlabeled learning framework that allows unbiased estimation of classification risk from samples with any number of complementary labels and unlabeled samples, for arbitrary loss functions and models. We first give an unbiased estimator of the classification risk from samples with multiple complementary labels, and then further improve the estimator by incorporating unlabeled samples into the risk formulation. The estimation error bounds show that the proposed methods are in the optimal parametric convergence rate. Finally, the experiments on both linear and deep models show the effectiveness of our methods.