Senlin Shu
An Unbiased Risk Estimator for Partial Label Learning with Augmented Classes
Sep 29, 2024Abstract:Partial Label Learning (PLL) is a typical weakly supervised learning task, which assumes each training instance is annotated with a set of candidate labels containing the ground-truth label. Recent PLL methods adopt identification-based disambiguation to alleviate the influence of false positive labels and achieve promising performance. However, they require all classes in the test set to have appeared in the training set, ignoring the fact that new classes will keep emerging in real applications. To address this issue, in this paper, we focus on the problem of Partial Label Learning with Augmented Class (PLLAC), where one or more augmented classes are not visible in the training stage but appear in the inference stage. Specifically, we propose an unbiased risk estimator with theoretical guarantees for PLLAC, which estimates the distribution of augmented classes by differentiating the distribution of known classes from unlabeled data and can be equipped with arbitrary PLL loss functions. Besides, we provide a theoretical analysis of the estimation error bound of the estimator, which guarantees the convergence of the empirical risk minimizer to the true risk minimizer as the number of training data tends to infinity. Furthermore, we add a risk-penalty regularization term in the optimization objective to alleviate the influence of the over-fitting issue caused by negative empirical risk. Extensive experiments on benchmark, UCI and real-world datasets demonstrate the effectiveness of the proposed approach.
A Generalized Unbiased Risk Estimator for Learning with Augmented Classes
Jun 12, 2023



Abstract:In contrast to the standard learning paradigm where all classes can be observed in training data, learning with augmented classes (LAC) tackles the problem where augmented classes unobserved in the training data may emerge in the test phase. Previous research showed that given unlabeled data, an unbiased risk estimator (URE) can be derived, which can be minimized for LAC with theoretical guarantees. However, this URE is only restricted to the specific type of one-versus-rest loss functions for multi-class classification, making it not flexible enough when the loss needs to be changed with the dataset in practice. In this paper, we propose a generalized URE that can be equipped with arbitrary loss functions while maintaining the theoretical guarantees, given unlabeled data for LAC. To alleviate the issue of negative empirical risk commonly encountered by previous studies, we further propose a novel risk-penalty regularization term. Experiments demonstrate the effectiveness of our proposed method.
Multi-Class Classification from Single-Class Data with Confidences
Jun 16, 2021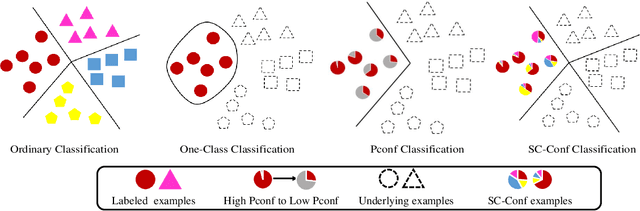


Abstract:Can we learn a multi-class classifier from only data of a single class? We show that without any assumptions on the loss functions, models, and optimizers, we can successfully learn a multi-class classifier from only data of a single class with a rigorous consistency guarantee when confidences (i.e., the class-posterior probabilities for all the classes) are available. Specifically, we propose an empirical risk minimization framework that is loss-/model-/optimizer-independent. Instead of constructing a boundary between the given class and other classes, our method can conduct discriminative classification between all the classes even if no data from the other classes are provided. We further theoretically and experimentally show that our method can be Bayes-consistent with a simple modification even if the provided confidences are highly noisy. Then, we provide an extension of our method for the case where data from a subset of all the classes are available. Experimental results demonstrate the effectiveness of our methods.
Pointwise Binary Classification with Pairwise Confidence Comparisons
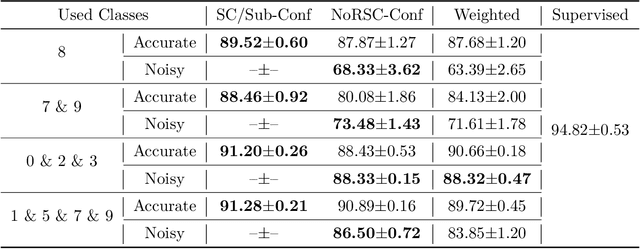
Oct 05, 2020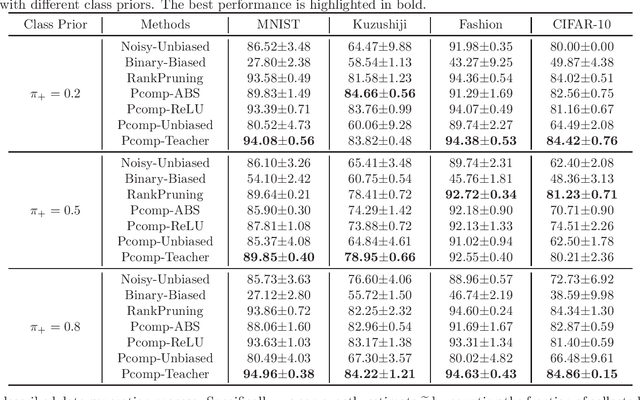
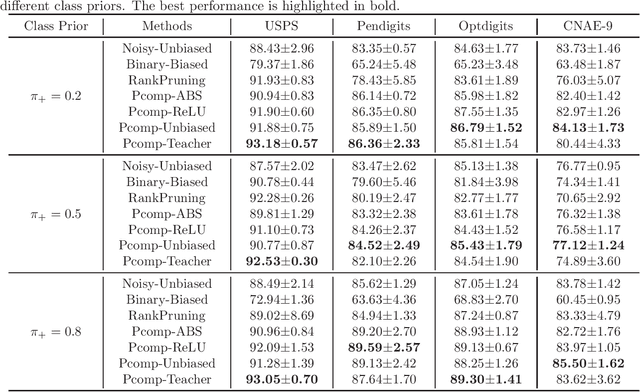

Abstract:Ordinary (pointwise) binary classification aims to learn a binary classifier from pointwise labeled data. However, such pointwise labels may not be directly accessible due to privacy, confidentiality, or security considerations. In this case, can we still learn an accurate binary classifier? This paper proposes a novel setting, namely pairwise comparison (Pcomp) classification, where we are given only pairs of unlabeled data that we know one is more likely to be positive than the other, instead of pointwise labeled data. Pcomp classification is useful for private or subjective classification tasks. To solve this problem, we present a mathematical formulation for the generation process of pairwise comparison data, based on which we exploit an unbiased risk estimator(URE) to train a binary classifier by empirical risk minimization and establish an estimation error bound. We first prove that a URE can be derived and improve it using correction functions. Then, we start from the noisy-label learning perspective to introduce a progressive URE and improve it by imposing consistency regularization. Finally, experiments validate the effectiveness of our proposed solutions for Pcomp classification.
Incorporating Multiple Cluster Centers for Multi-Label Learning
Apr 17, 2020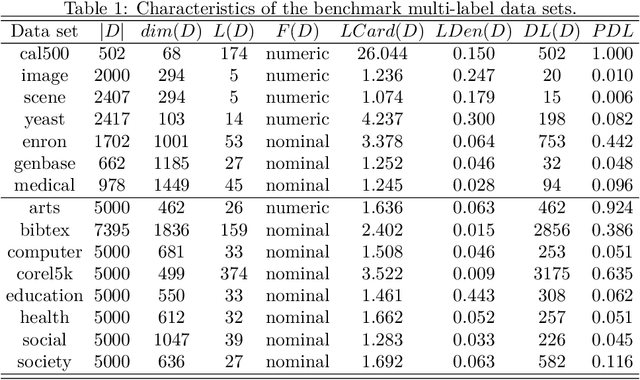
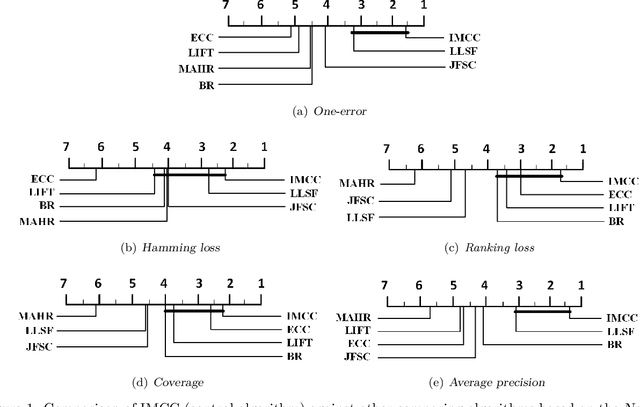
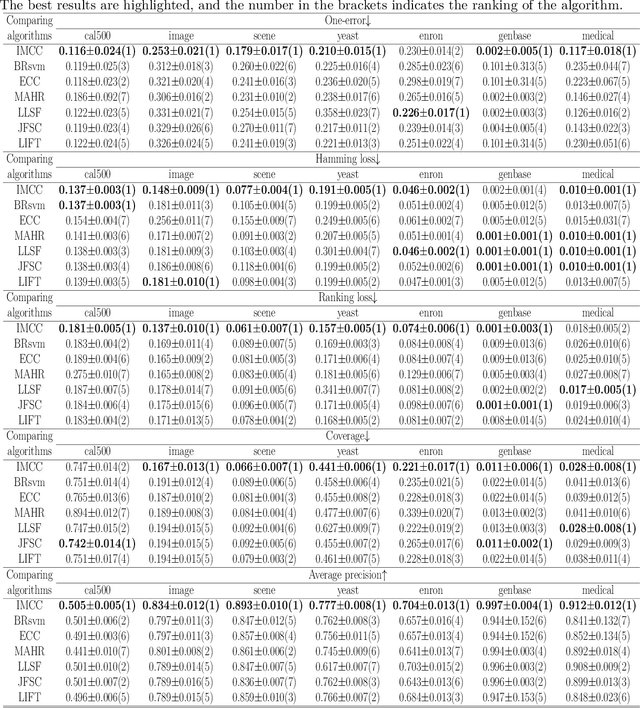
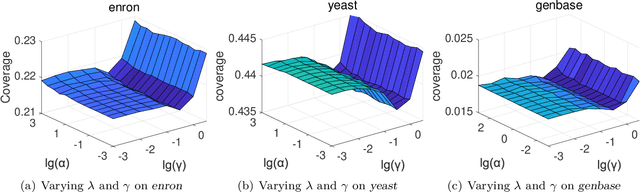
Abstract:Multi-label learning deals with the problem that each instance is associated with multiple labels simultaneously. Most of the existing approaches aim to improve the performance of multi-label learning by exploiting label correlations. Although the data augmentation technique is widely used in many machine learning tasks, it is still unclear whether data augmentation is helpful to multi-label learning. In this paper, (to the best of our knowledge) we provide the first attempt to leverage the data augmentation technique to improve the performance of multi-label learning. Specifically, we first propose a novel data augmentation approach that performs clustering on the real examples and treats the cluster centers as virtual examples, and these virtual examples naturally embody the local label correlations and label importances. Then, motivated by the cluster assumption that examples in the same cluster should have the same label, we propose a novel regularization term to bridge the gap between the real examples and virtual examples, which can promote the local smoothness of the learning function. Extensive experimental results on a number of real-world multi-label data sets clearly demonstrate that our proposed approach outperforms the state-of-the-art counterparts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge