Unsupervised linear component analysis for a class of probability mixture models

We deal with a model where a set of observations is obtained by a linear superposition of unknown components called sources. The problem consists in recovering the sources without knowing the linear transform. We extend the well-known Independent Component Analysis (ICA) methodology. Instead of assuming independent source components, we assume that the source vector is a probability mixture of two distributions. Only one distribution satisfies the ICA assumptions, while the other one is concentrated on a specific but unknown support. Sample points from the latter are clustered based on a data-driven distance in a fully unsupervised approach. A theoretical grounding is provided through a link with the Christoffel function. Simulation results validate our approach and illustrate that it is an extension of a formerly proposed method.

Sparse Signal Reconstruction for Nonlinear Models via Piecewise Rational Optimization

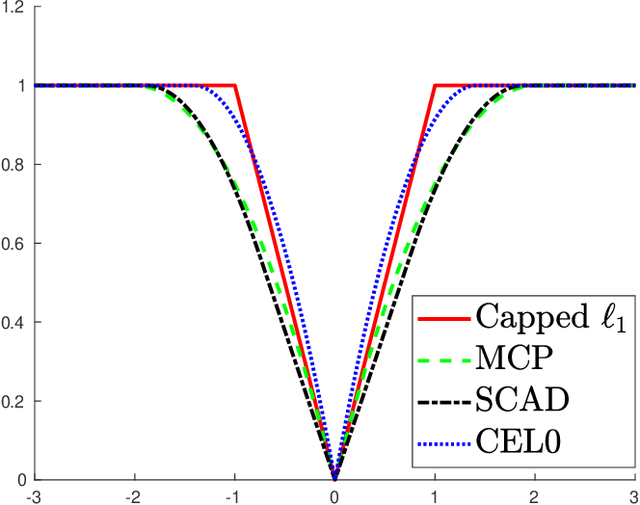
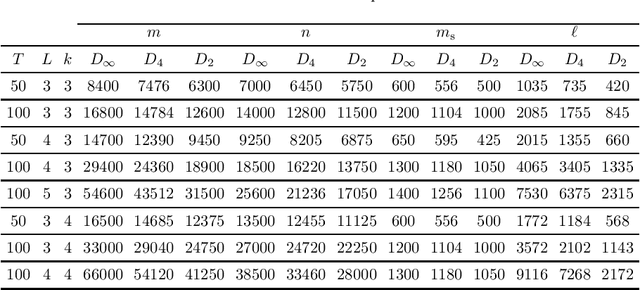
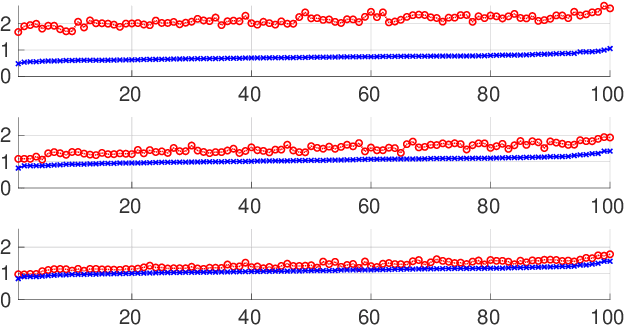
We propose a method to reconstruct sparse signals degraded by a nonlinear distortion and acquired at a limited sampling rate. Our method formulates the reconstruction problem as a nonconvex minimization of the sum of a data fitting term and a penalization term. In contrast with most previous works which settle for approximated local solutions, we seek for a global solution to the obtained challenging nonconvex problem. Our global approach relies on the so-called Lasserre relaxation of polynomial optimization. We here specifically include in our approach the case of piecewise rational functions, which makes it possible to address a wide class of nonconvex exact and continuous relaxations of the $\ell_0$ penalization function. Additionally, we study the complexity of the optimization problem. It is shown how to use the structure of the problem to lighten the computational burden efficiently. Finally, numerical simulations illustrate the benefits of our method in terms of both global optimality and signal reconstruction.

Modeling Electrical Motor Dynamics using Encoder-Decoder with Recurrent Skip Connection

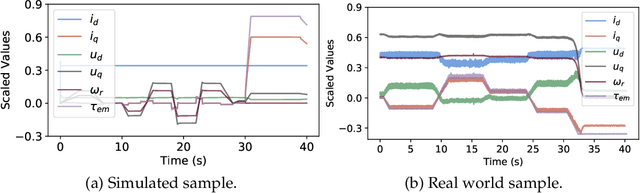
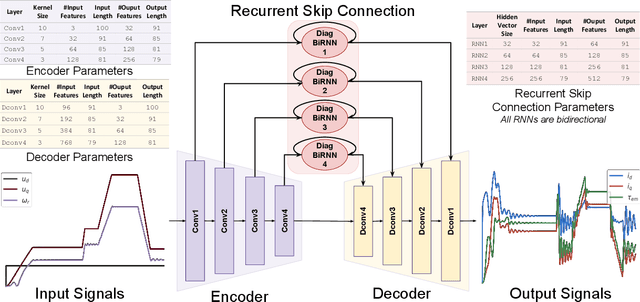
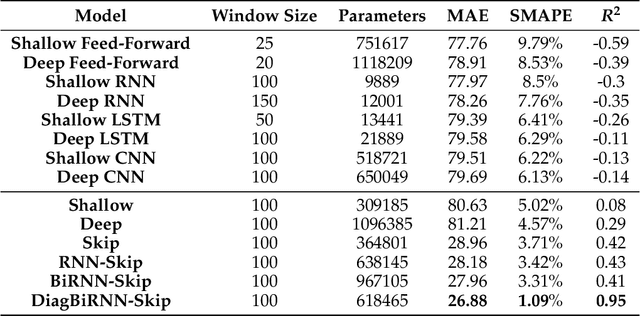
Electrical motors are the most important source of mechanical energy in the industrial world. Their modeling traditionally relies on a physics-based approach, which aims at taking their complex internal dynamics into account. In this paper, we explore the feasibility of modeling the dynamics of an electrical motor by following a data-driven approach, which uses only its inputs and outputs and does not make any assumption on its internal behaviour. We propose a novel encoder-decoder architecture which benefits from recurrent skip connections. We also propose a novel loss function that takes into account the complexity of electrical motor quantities and helps in avoiding model bias. We show that the proposed architecture can achieve a good learning performance on our high-frequency high-variance datasets. Two datasets are considered: the first one is generated using a simulator based on the physics of an induction motor and the second one is recorded from an industrial electrical motor. We benchmark our solution using variants of traditional neural networks like feedforward, convolutional, and recurrent networks. We evaluate various design choices of our architecture and compare it to the baselines. We show the domain adaptation capability of our model to learn dynamics just from simulated data by testing it on the raw sensor data. We finally show the effect of signal complexity on the proposed method ability to model temporal dynamics.