Majorization-minimization for Sparse Nonnegative Matrix Factorization with the $β$-divergence
Paper and Code
Jul 13, 2022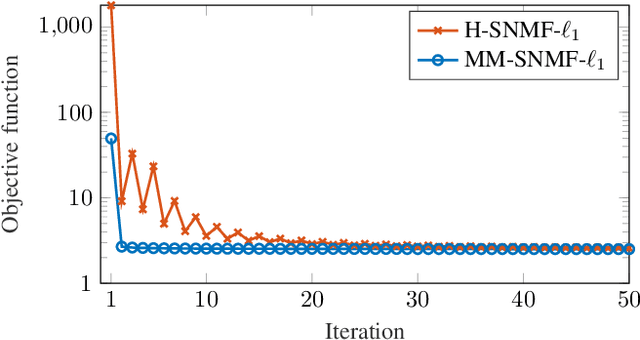
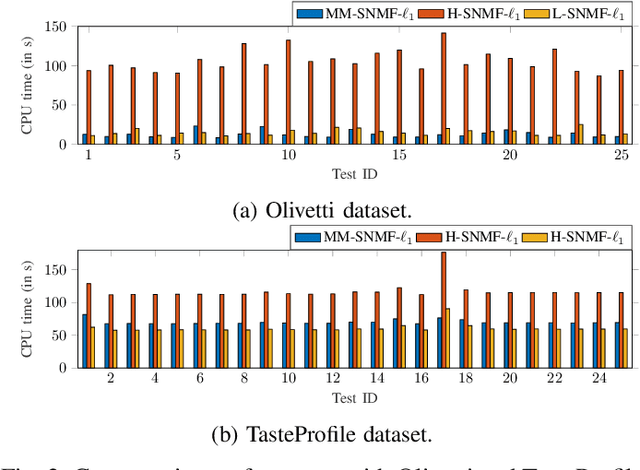
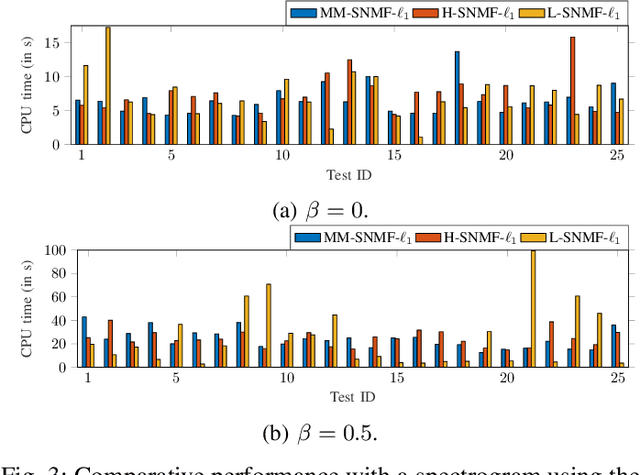
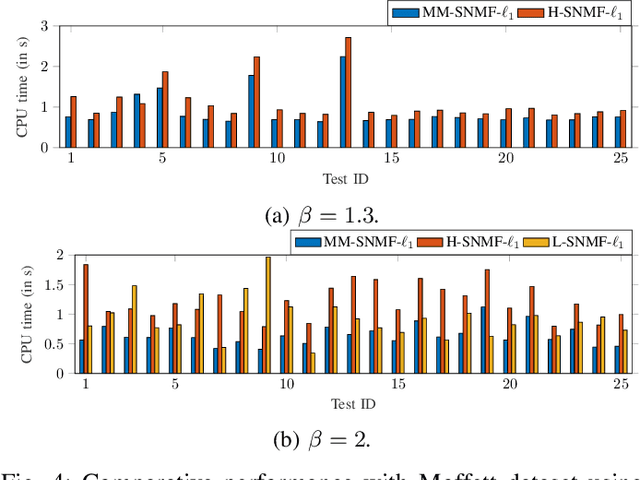
This article introduces new multiplicative updates for nonnegative matrix factorization with the $\beta$-divergence and sparse regularization of one of the two factors (say, the activation matrix). It is well known that the norm of the other factor (the dictionary matrix) needs to be controlled in order to avoid an ill-posed formulation. Standard practice consists in constraining the columns of the dictionary to have unit norm, which leads to a nontrivial optimization problem. Our approach leverages a reparametrization of the original problem into the optimization of an equivalent scale-invariant objective function. From there, we derive block-descent majorization-minimization algorithms that result in simple multiplicative updates for either $\ell_{1}$-regularization or the more "aggressive" log-regularization. In contrast with other state-of-the-art methods, our algorithms are universal in the sense that they can be applied to any $\beta$-divergence (i.e., any value of $\beta$) and that they come with convergence guarantees. We report numerical comparisons with existing heuristic and Lagrangian methods using various datasets: face images, an audio spectrogram, hyperspectral data, and song play counts. We show that our methods obtain solutions of similar quality at convergence (similar objective values) but with significantly reduced CPU times.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge