Algorithms for audio inpainting based on probabilistic nonnegative matrix factorization
Paper and Code
Jun 28, 2022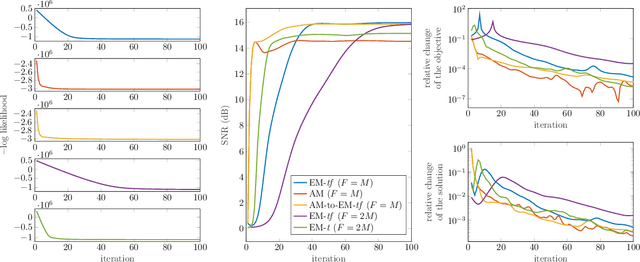

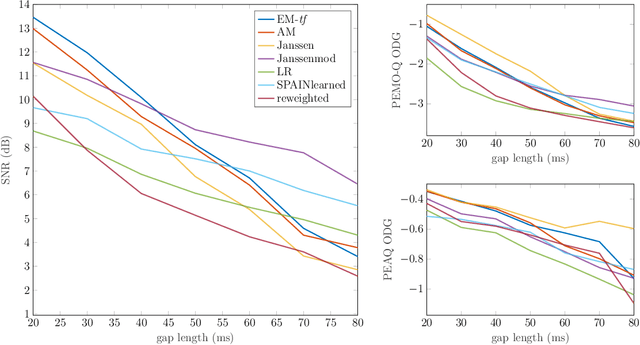
Audio inpainting, i.e., the task of restoring missing or occluded audio signal samples, usually relies on sparse representations or autoregressive modeling. In this paper, we propose to structure the spectrogram with nonnegative matrix factorization (NMF) in a probabilistic framework. First, we treat the missing samples as latent variables, and derive two expectation-maximization algorithms for estimating the parameters of the model, depending on whether we formulate the problem in the time- or time-frequency domain. Then, we treat the missing samples as parameters, and we address this novel problem by deriving an alternating minimization scheme. We assess the potential of these algorithms for the task of restoring short- to middle-length gaps in music signals. Experiments reveal great convergence properties of the proposed methods, as well as competitive performance when compared to state-of-the-art audio inpainting techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge