A majorization-minimization algorithm for nonnegative binary matrix factorization
Paper and Code
Apr 20, 2022
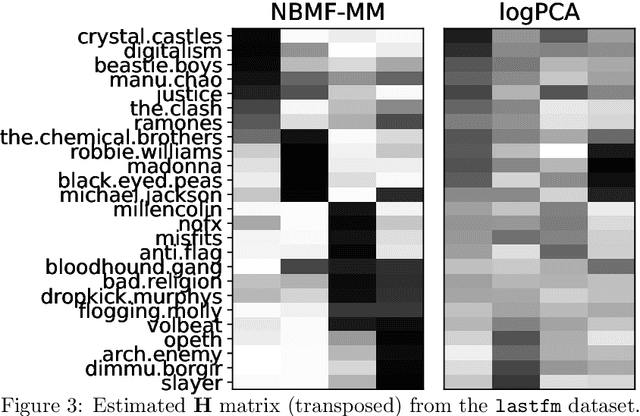
This paper tackles the problem of decomposing binary data using matrix factorization. We consider the family of mean-parametrized Bernoulli models, a class of generative models that are well suited for modeling binary data and enables interpretability of the factors. We factorize the Bernoulli parameter and consider an additional Beta prior on one of the factors to further improve the model's expressive power. While similar models have been proposed in the literature, they only exploit the Beta prior as a proxy to ensure a valid Bernoulli parameter in a Bayesian setting; in practice it reduces to a uniform or uninformative prior. Besides, estimation in these models has focused on costly Bayesian inference. In this paper, we propose a simple yet very efficient majorization-minimization algorithm for maximum a posteriori estimation. Our approach leverages the Beta prior whose parameters can be tuned to improve performance in matrix completion tasks. Experiments conducted on three public binary datasets show that our approach offers an excellent trade-off between prediction performance, computational complexity, and interpretability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge