Junbo Duan
Homotopy based algorithms for $\ell_0$-regularized least-squares
Mar 18, 2015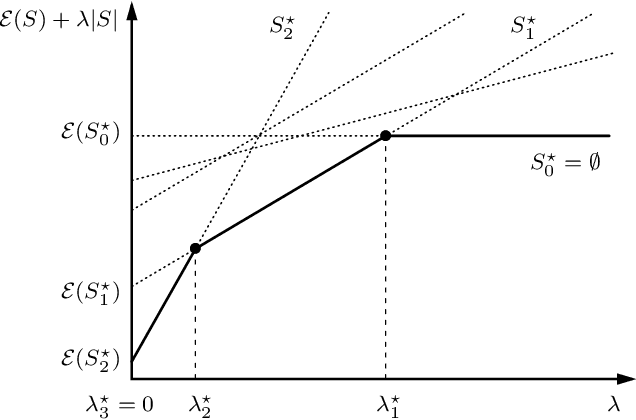
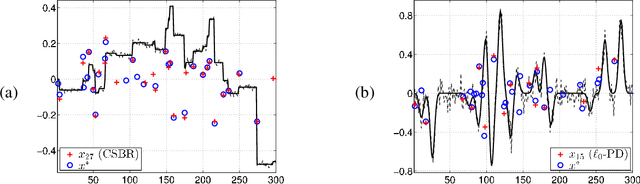
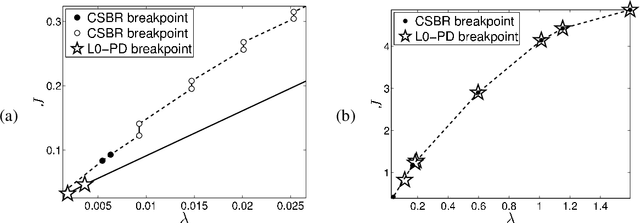

Abstract:Sparse signal restoration is usually formulated as the minimization of a quadratic cost function $\|y-Ax\|_2^2$, where A is a dictionary and x is an unknown sparse vector. It is well-known that imposing an $\ell_0$ constraint leads to an NP-hard minimization problem. The convex relaxation approach has received considerable attention, where the $\ell_0$-norm is replaced by the $\ell_1$-norm. Among the many efficient $\ell_1$ solvers, the homotopy algorithm minimizes $\|y-Ax\|_2^2+\lambda\|x\|_1$ with respect to x for a continuum of $\lambda$'s. It is inspired by the piecewise regularity of the $\ell_1$-regularization path, also referred to as the homotopy path. In this paper, we address the minimization problem $\|y-Ax\|_2^2+\lambda\|x\|_0$ for a continuum of $\lambda$'s and propose two heuristic search algorithms for $\ell_0$-homotopy. Continuation Single Best Replacement is a forward-backward greedy strategy extending the Single Best Replacement algorithm, previously proposed for $\ell_0$-minimization at a given $\lambda$. The adaptive search of the $\lambda$-values is inspired by $\ell_1$-homotopy. $\ell_0$ Regularization Path Descent is a more complex algorithm exploiting the structural properties of the $\ell_0$-regularization path, which is piecewise constant with respect to $\lambda$. Both algorithms are empirically evaluated for difficult inverse problems involving ill-conditioned dictionaries. Finally, we show that they can be easily coupled with usual methods of model order selection.
* 38 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge