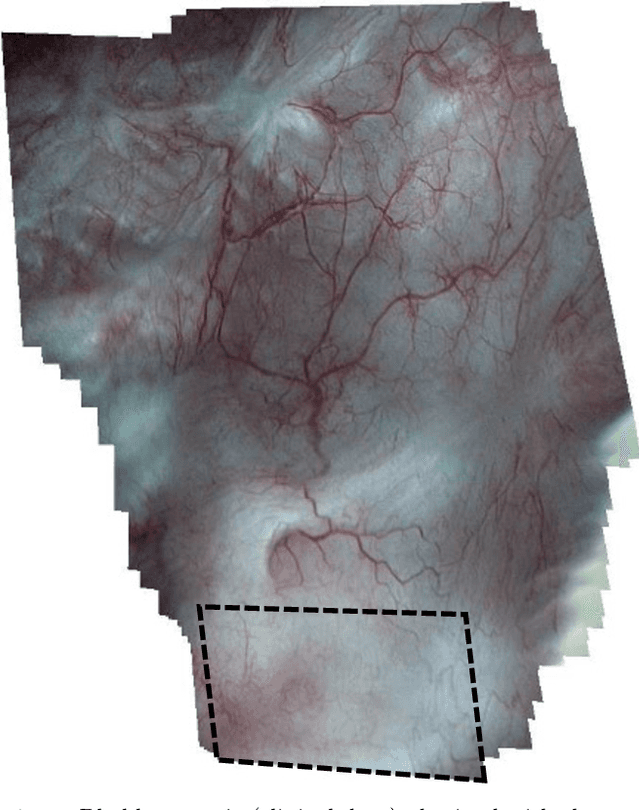
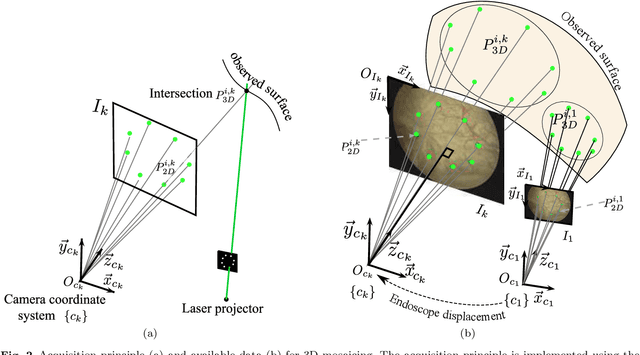
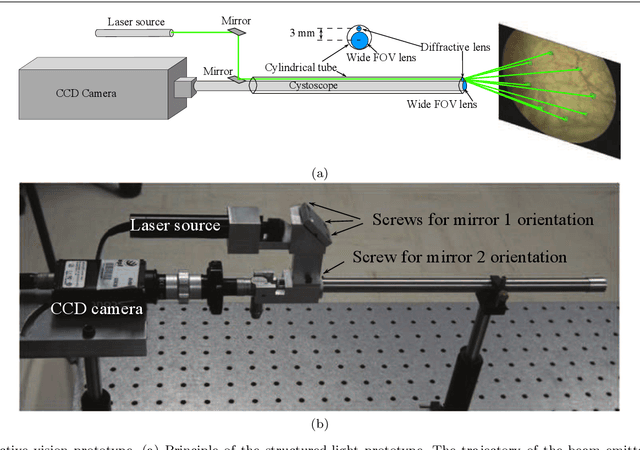
Construction of extended 3D field of views of the internal bladder wall surface: a proof of concept

3D extended field of views (FOVs) of the internal bladder wall facilitate lesion diagnosis, patient follow-up and treatment traceability. In this paper, we propose a 3D image mosaicing algorithm guided by 2D cystoscopic video-image registration for obtaining textured FOV mosaics. In this feasibility study, the registration makes use of data from a 3D cystoscope prototype providing, in addition to each small FOV image, some 3D points located on the surface. This proof of concept shows that textured surfaces can be constructed with minimally modified cystoscopes. The potential of the method is demonstrated on numerical and real phantoms reproducing various surface shapes. Pig and human bladder textures are superimposed on phantoms with known shape and dimensions. These data allow for quantitative assessment of the 3D mosaicing algorithm based on the registration of images simulating bladder textures.

Comparative study of image registration techniques for bladder video-endoscopy

Bladder cancer is widely spread in the world. Many adequate diagnosis techniques exist. Video-endoscopy remains the standard clinical procedure for visual exploration of the bladder internal surface. However, video-endoscopy presents the limit that the imaged area for each image is about nearly 1cm2. And, lesions are, typically, spread over several images. The aim of this contribution is to assess the performance of two mosaicing algorithms leading to the construction of panoramic maps (one unique image) of bladder walls. The quantitative comparison study is performed on a set of real endoscopic exam data and on simulated data relative to bladder phantom.

Homotopy based algorithms for $\ell_0$-regularized least-squares

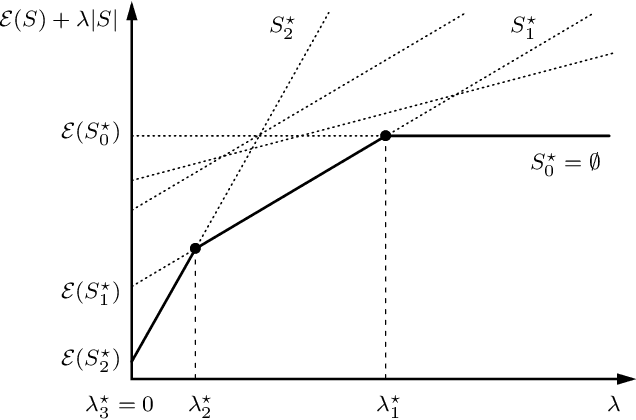
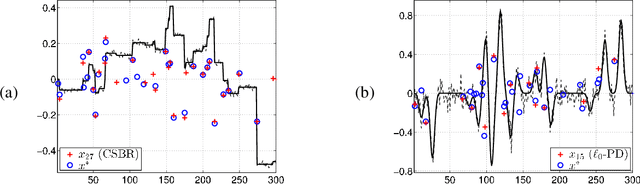
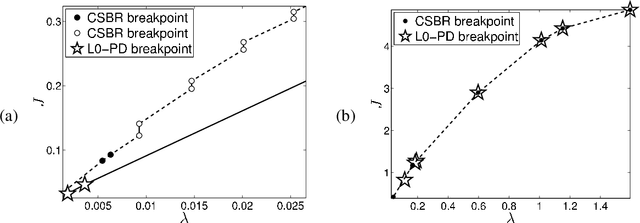
Sparse signal restoration is usually formulated as the minimization of a quadratic cost function $\|y-Ax\|_2^2$, where A is a dictionary and x is an unknown sparse vector. It is well-known that imposing an $\ell_0$ constraint leads to an NP-hard minimization problem. The convex relaxation approach has received considerable attention, where the $\ell_0$-norm is replaced by the $\ell_1$-norm. Among the many efficient $\ell_1$ solvers, the homotopy algorithm minimizes $\|y-Ax\|_2^2+\lambda\|x\|_1$ with respect to x for a continuum of $\lambda$'s. It is inspired by the piecewise regularity of the $\ell_1$-regularization path, also referred to as the homotopy path. In this paper, we address the minimization problem $\|y-Ax\|_2^2+\lambda\|x\|_0$ for a continuum of $\lambda$'s and propose two heuristic search algorithms for $\ell_0$-homotopy. Continuation Single Best Replacement is a forward-backward greedy strategy extending the Single Best Replacement algorithm, previously proposed for $\ell_0$-minimization at a given $\lambda$. The adaptive search of the $\lambda$-values is inspired by $\ell_1$-homotopy. $\ell_0$ Regularization Path Descent is a more complex algorithm exploiting the structural properties of the $\ell_0$-regularization path, which is piecewise constant with respect to $\lambda$. Both algorithms are empirically evaluated for difficult inverse problems involving ill-conditioned dictionaries. Finally, we show that they can be easily coupled with usual methods of model order selection.

A sufficient condition on monotonic increase of the number of nonzero entry in the optimizer of L1 norm penalized least-square problem

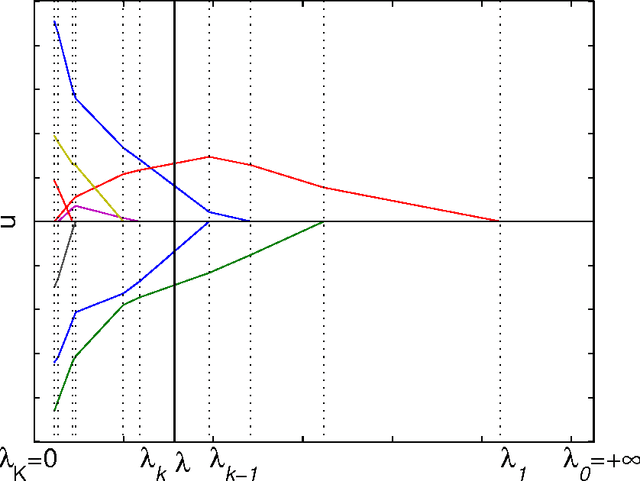
The $\ell$-1 norm based optimization is widely used in signal processing, especially in recent compressed sensing theory. This paper studies the solution path of the $\ell$-1 norm penalized least-square problem, whose constrained form is known as Least Absolute Shrinkage and Selection Operator (LASSO). A solution path is the set of all the optimizers with respect to the evolution of the hyperparameter (Lagrange multiplier). The study of the solution path is of great significance in viewing and understanding the profile of the tradeoff between the approximation and regularization terms. If the solution path of a given problem is known, it can help us to find the optimal hyperparameter under a given criterion such as the Akaike Information Criterion. In this paper we present a sufficient condition on $\ell$-1 norm penalized least-square problem. Under this sufficient condition, the number of nonzero entries in the optimizer or solution vector increases monotonically when the hyperparameter decreases. We also generalize the result to the often used total variation case, where the $\ell$-1 norm is taken over the first order derivative of the solution vector. We prove that the proposed condition has intrinsic connections with the condition given by Donoho, et al \cite{Donoho08} and the positive cone condition by Efron {\it el al} \cite{Efron04}. However, the proposed condition does not need to assume the sparsity level of the signal as required by Donoho et al's condition, and is easier to verify than Efron, et al's positive cone condition when being used for practical applications.