Jerome Idier
A sufficient condition on monotonic increase of the number of nonzero entry in the optimizer of L1 norm penalized least-square problem
Apr 19, 2011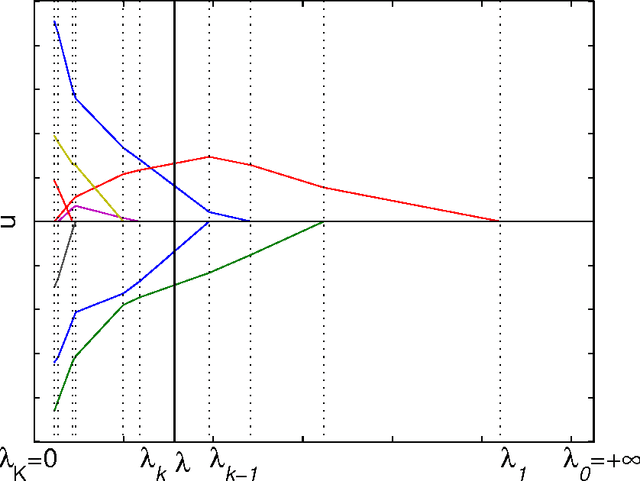
Abstract:The $\ell$-1 norm based optimization is widely used in signal processing, especially in recent compressed sensing theory. This paper studies the solution path of the $\ell$-1 norm penalized least-square problem, whose constrained form is known as Least Absolute Shrinkage and Selection Operator (LASSO). A solution path is the set of all the optimizers with respect to the evolution of the hyperparameter (Lagrange multiplier). The study of the solution path is of great significance in viewing and understanding the profile of the tradeoff between the approximation and regularization terms. If the solution path of a given problem is known, it can help us to find the optimal hyperparameter under a given criterion such as the Akaike Information Criterion. In this paper we present a sufficient condition on $\ell$-1 norm penalized least-square problem. Under this sufficient condition, the number of nonzero entries in the optimizer or solution vector increases monotonically when the hyperparameter decreases. We also generalize the result to the often used total variation case, where the $\ell$-1 norm is taken over the first order derivative of the solution vector. We prove that the proposed condition has intrinsic connections with the condition given by Donoho, et al \cite{Donoho08} and the positive cone condition by Efron {\it el al} \cite{Efron04}. However, the proposed condition does not need to assume the sparsity level of the signal as required by Donoho et al's condition, and is easier to verify than Efron, et al's positive cone condition when being used for practical applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge