A Partially Collapsed Sampler for Unsupervised Nonnegative Spike Train Restoration
Paper and Code
Feb 11, 2021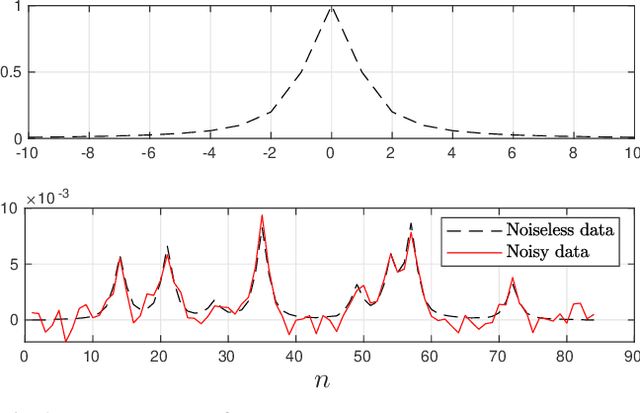
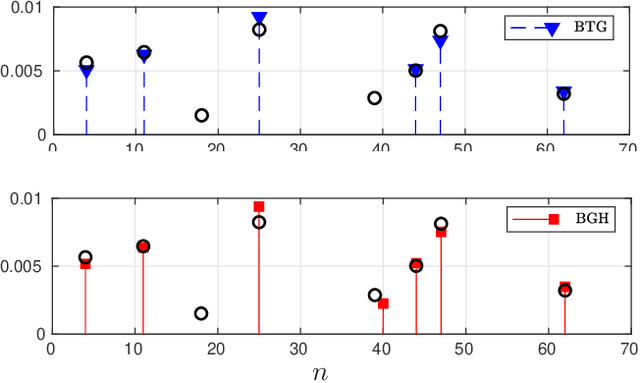
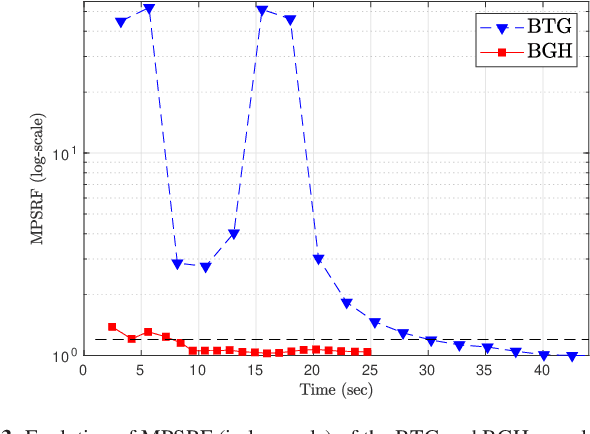
In this paper the problem of restoration of non-negative sparse signals is addressed in the Bayesian framework. We introduce a new probabilistic hierarchical prior, based on the Generalized Hyperbolic (GH) distribution, which explicitly accounts for sparsity. This new prior allows on the one hand, to take into account the non-negativity. And on the other hand, thanks to the decomposition of GH distributions as continuous Gaussian mean-variance mixture, allows us to propose a partially collapsed Gibbs sampler (PCGS), which is shown to be more efficient in terms of convergence time than the classical Gibbs sampler.
* in Proceedings of iTWIST'20, Paper-ID: 14, Nantes, France, December,
2-4, 2020
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge