Identifiability of Low-Rank Sparse Component Analysis
Paper and Code
Aug 27, 2018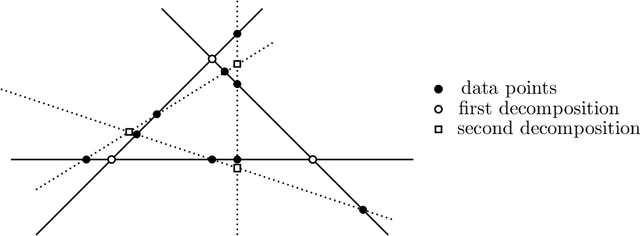
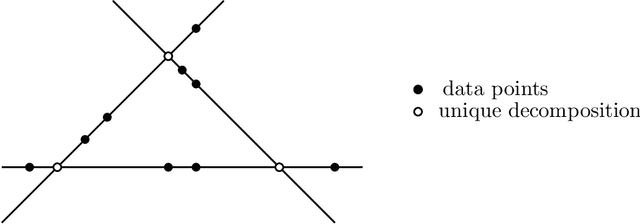
Sparse component analysis (SCA) is the following problem: Given an input matrix $M$ and an integer $r$, find a dictionary $D$ with $r$ columns and a sparse matrix $B$ with $r$ rows such that $M \approx DB$. A key issue in SCA is identifiability, that is, characterizing the conditions under which $D$ and $B$ are essentially unique (that is, they are unique up to permutation and scaling of the columns of $D$ and rows of $B$). Although SCA has been vastly investigated in the last two decades, only a few works have tackled this issue in the deterministic scenario, and no work provides reasonable bounds in the minimum number of data points (that is, columns of $M$) that leads to identifiability. In this work, we provide new results in the deterministic scenario when the data has a low-rank structure, that is, when $D$ has rank $r$, drastically improving with respect to previous results. In particular, we show that if each column of $B$ contains at least $s$ zeros then $\mathcal{O}(r^3/s^2)$ data points are sufficient to obtain an essentially unique decomposition, as long as these data points are well spread among the subspaces spanned by $r-1$ columns of $D$. This implies for example that for a fixed proportion of zeros (constant and independent of $r$, e.g., 10\% of zero entries in $B$), one only requires $O(r)$ data points to guarantee identifiability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge