FCNCP: A Coupled Nonnegative CANDECOMP/PARAFAC Decomposition Based on Federated Learning

In the field of brain science, data sharing across servers is becoming increasingly challenging due to issues such as industry competition, privacy security, and administrative procedure policies and regulations. Therefore, there is an urgent need to develop new methods for data analysis and processing that enable scientific collaboration without data sharing. In view of this, this study proposes to study and develop a series of efficient non-negative coupled tensor decomposition algorithm frameworks based on federated learning called FCNCP for the EEG data arranged on different servers. It combining the good discriminative performance of tensor decomposition in high-dimensional data representation and decomposition, the advantages of coupled tensor decomposition in cross-sample tensor data analysis, and the features of federated learning for joint modelling in distributed servers. The algorithm utilises federation learning to establish coupling constraints for data distributed across different servers. In the experiments, firstly, simulation experiments are carried out using simulated data, and stable and consistent decomposition results are obtained, which verify the effectiveness of the proposed algorithms in this study. Then the FCNCP algorithm was utilised to decompose the fifth-order event-related potential (ERP) tensor data collected by applying proprioceptive stimuli on the left and right hands. It was found that contralateral stimulation induced more symmetrical components in the activation areas of the left and right hemispheres. The conclusions drawn are consistent with the interpretations of related studies in cognitive neuroscience, demonstrating that the method can efficiently process higher-order EEG data and that some key hidden information can be preserved.

Fast Learnings of Coupled Nonnegative Tensor Decomposition Using Optimal Gradient and Low-rank Approximation

Nonnegative tensor decomposition has been widely applied in signal processing and neuroscience, etc. When it comes to group analysis of multi-block tensors, traditional tensor decomposition is insufficient to utilize the shared/similar information among tensors. In this study, we propose a coupled nonnegative CANDECOMP/PARAFAC decomposition algorithm optimized by the alternating proximal gradient method (CoNCPDAPG), which is capable of a simultaneous decomposition of tensors from different samples that are partially linked and a simultaneous extraction of common components, individual components and core tensors. Due to the low optimization efficiency brought by the nonnegative constraint and the high-dimensional nature of the data, we further propose the lraCoNCPD-APG algorithm by combining low-rank approximation and the proposed CoNCPD-APG method. When processing multi-block large-scale tensors, the proposed lraCoNCPD-APG algorithm can greatly reduce the computational load without compromising the decomposition quality. Experiment results of coupled nonnegative tensor decomposition problems designed for synthetic data, real-world face images and event-related potential data demonstrate the practicability and superiority of the proposed algorithms.

PARAFAC2-based Coupled Matrix and Tensor Factorizations

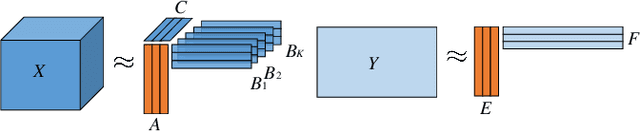
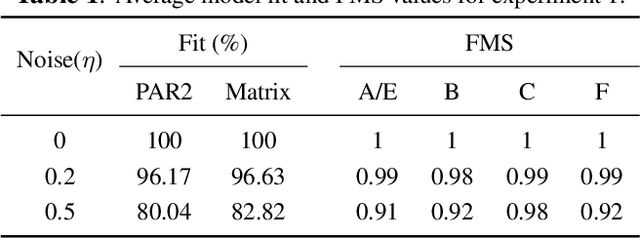
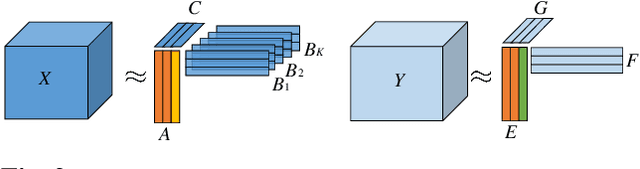
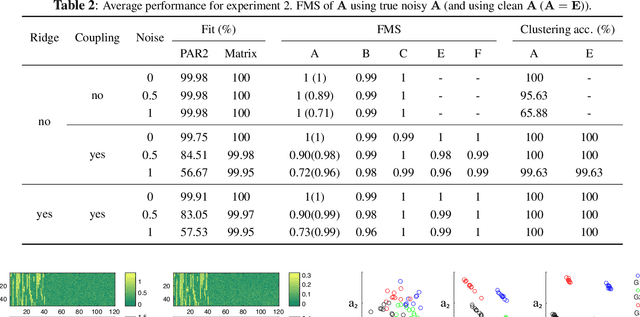
Coupled matrix and tensor factorizations (CMTF) have emerged as an effective data fusion tool to jointly analyze data sets in the form of matrices and higher-order tensors. The PARAFAC2 model has shown to be a promising alternative to the CANDECOMP/PARAFAC (CP) tensor model due to its flexibility and capability to handle irregular/ragged tensors. While fusion models based on a PARAFAC2 model coupled with matrix/tensor decompositions have been recently studied, they are limited in terms of possible regularizations and/or types of coupling between data sets. In this paper, we propose an algorithmic framework for fitting PARAFAC2-based CMTF models with the possibility of imposing various constraints on all modes and linear couplings, using Alternating Optimization (AO) and the Alternating Direction Method of Multipliers (ADMM). Through numerical experiments, we demonstrate that the proposed algorithmic approach accurately recovers the underlying patterns using various constraints and linear couplings.