Fast Learnings of Coupled Nonnegative Tensor Decomposition Using Optimal Gradient and Low-rank Approximation

Nonnegative tensor decomposition has been widely applied in signal processing and neuroscience, etc. When it comes to group analysis of multi-block tensors, traditional tensor decomposition is insufficient to utilize the shared/similar information among tensors. In this study, we propose a coupled nonnegative CANDECOMP/PARAFAC decomposition algorithm optimized by the alternating proximal gradient method (CoNCPDAPG), which is capable of a simultaneous decomposition of tensors from different samples that are partially linked and a simultaneous extraction of common components, individual components and core tensors. Due to the low optimization efficiency brought by the nonnegative constraint and the high-dimensional nature of the data, we further propose the lraCoNCPD-APG algorithm by combining low-rank approximation and the proposed CoNCPD-APG method. When processing multi-block large-scale tensors, the proposed lraCoNCPD-APG algorithm can greatly reduce the computational load without compromising the decomposition quality. Experiment results of coupled nonnegative tensor decomposition problems designed for synthetic data, real-world face images and event-related potential data demonstrate the practicability and superiority of the proposed algorithms.

Sparse Nonnegative CANDECOMP/PARAFAC Decomposition in Block Coordinate Descent Framework: A Comparison Study

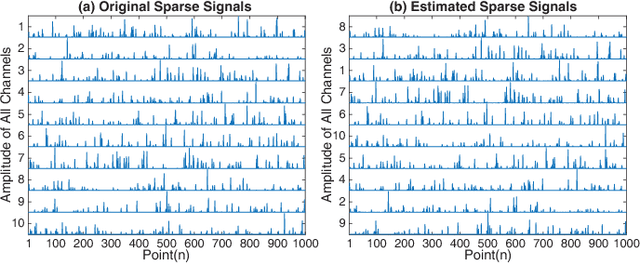
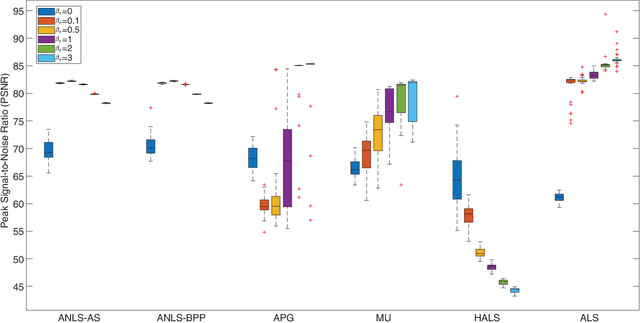
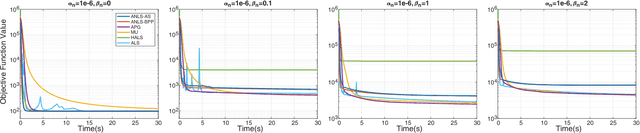
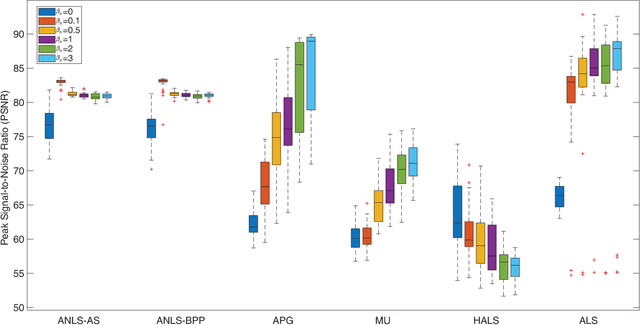
Nonnegative CANDECOMP/PARAFAC (NCP) decomposition is an important tool to process nonnegative tensor. Sometimes, additional sparse regularization is needed to extract meaningful nonnegative and sparse components. Thus, an optimization method for NCP that can impose sparsity efficiently is required. In this paper, we construct NCP with sparse regularization (sparse NCP) by l1-norm. Several popular optimization methods in block coordinate descent framework are employed to solve the sparse NCP, all of which are deeply analyzed with mathematical solutions. We compare these methods by experiments on synthetic and real tensor data, both of which contain third-order and fourth-order cases. After comparison, the methods that have fast computation and high effectiveness to impose sparsity will be concluded. In addition, we proposed an accelerated method to compute the objective function and relative error of sparse NCP, which has significantly improved the computation of tensor decomposition especially for higher-order tensor.

Diffusion map for clustering fMRI spatial maps extracted by independent component analysis

Functional magnetic resonance imaging (fMRI) produces data about activity inside the brain, from which spatial maps can be extracted by independent component analysis (ICA). In datasets, there are n spatial maps that contain p voxels. The number of voxels is very high compared to the number of analyzed spatial maps. Clustering of the spatial maps is usually based on correlation matrices. This usually works well, although such a similarity matrix inherently can explain only a certain amount of the total variance contained in the high-dimensional data where n is relatively small but p is large. For high-dimensional space, it is reasonable to perform dimensionality reduction before clustering. In this research, we used the recently developed diffusion map for dimensionality reduction in conjunction with spectral clustering. This research revealed that the diffusion map based clustering worked as well as the more traditional methods, and produced more compact clusters when needed.