Sparse Nonnegative CANDECOMP/PARAFAC Decomposition in Block Coordinate Descent Framework: A Comparison Study

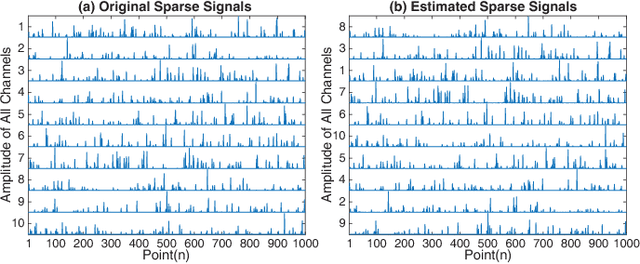
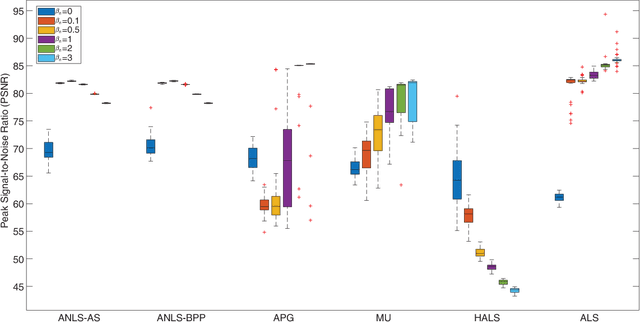
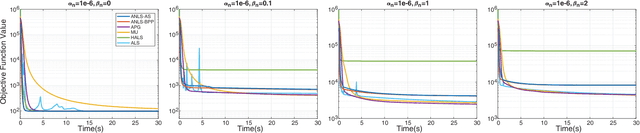
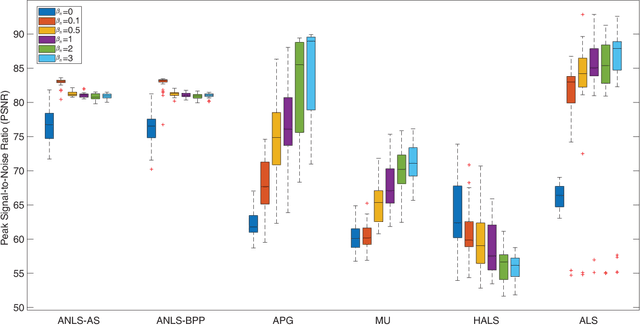
Nonnegative CANDECOMP/PARAFAC (NCP) decomposition is an important tool to process nonnegative tensor. Sometimes, additional sparse regularization is needed to extract meaningful nonnegative and sparse components. Thus, an optimization method for NCP that can impose sparsity efficiently is required. In this paper, we construct NCP with sparse regularization (sparse NCP) by l1-norm. Several popular optimization methods in block coordinate descent framework are employed to solve the sparse NCP, all of which are deeply analyzed with mathematical solutions. We compare these methods by experiments on synthetic and real tensor data, both of which contain third-order and fourth-order cases. After comparison, the methods that have fast computation and high effectiveness to impose sparsity will be concluded. In addition, we proposed an accelerated method to compute the objective function and relative error of sparse NCP, which has significantly improved the computation of tensor decomposition especially for higher-order tensor.