Adaptive directional Haar tight framelets on bounded domains for digraph signal representations

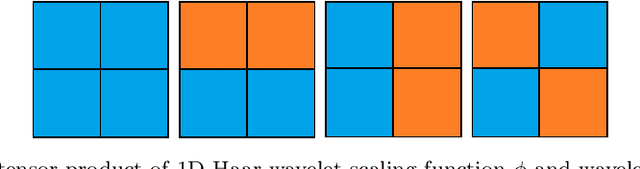
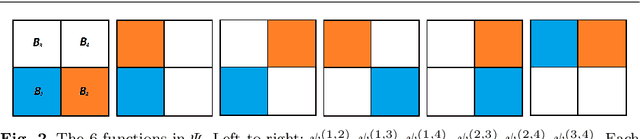
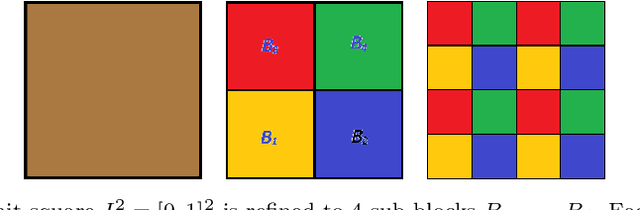
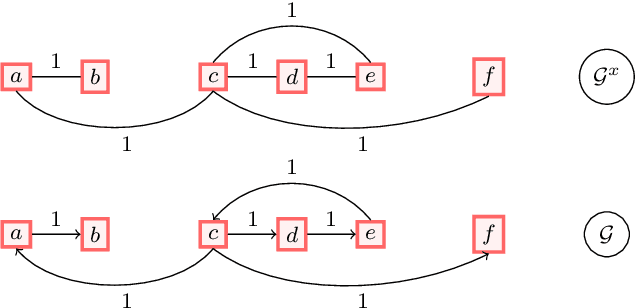
Based on hierarchical partitions, we provide the construction of Haar-type tight framelets on any compact set $K\subseteq \mathbb{R}^d$. In particular, on the unit block $[0,1]^d$, such tight framelets can be built to be with adaptivity and directionality. We show that the adaptive directional Haar tight framelet systems can be used for digraph signal representations. Some examples are provided to illustrate results in this paper.