Ruigang Zheng
Subgraph-based Tight Frames on Graphs with Compact Supports and Vanishing Moments
Sep 07, 2023



Abstract:In this work, we proposed a novel and general method to construct tight frames on graphs with compact supports based on a series of hierarchical partitions. Starting from our abstract construction that generalizes previous methods based on partition trees, we are able to flexibly incorporate subgraph Laplacians into our design of graph frames. Consequently, our general methods permit adjusting the (subgraph) vanishing moments of the framelets and extra properties, such as directionality, for efficiently representing graph signals with path-like supports. Several variants are explicitly defined and tested. Experimental results show our proposed graph frames perform superiorly in non-linear approximation tasks.
Permutation Equivariant Graph Framelets for Heterophilous Graph Learning
Jun 27, 2023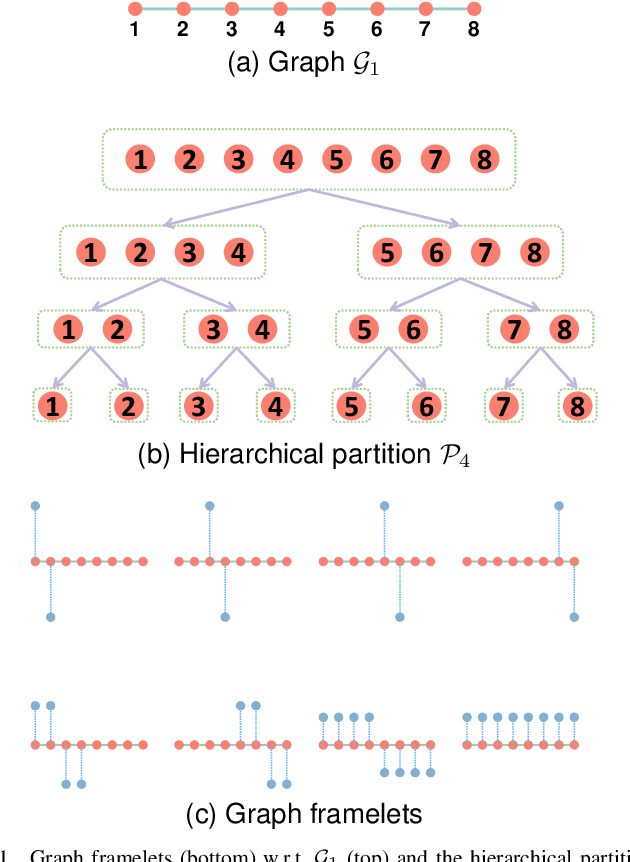
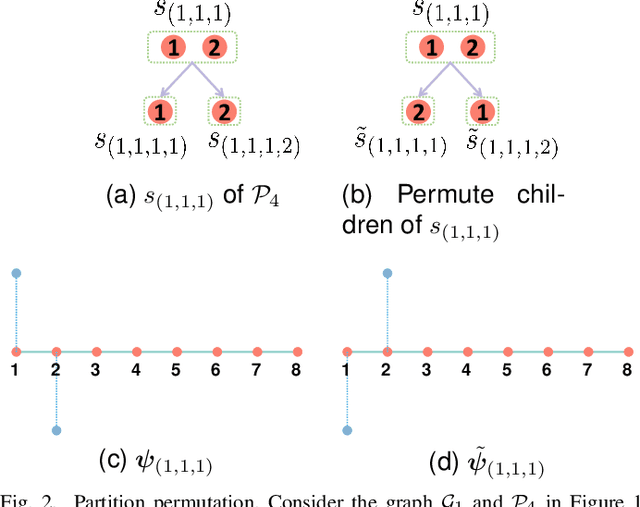
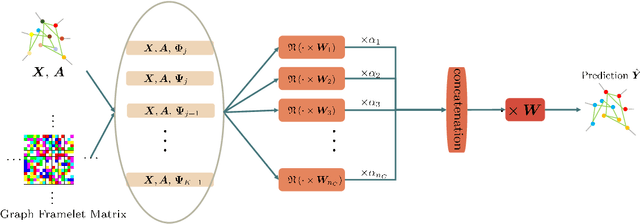
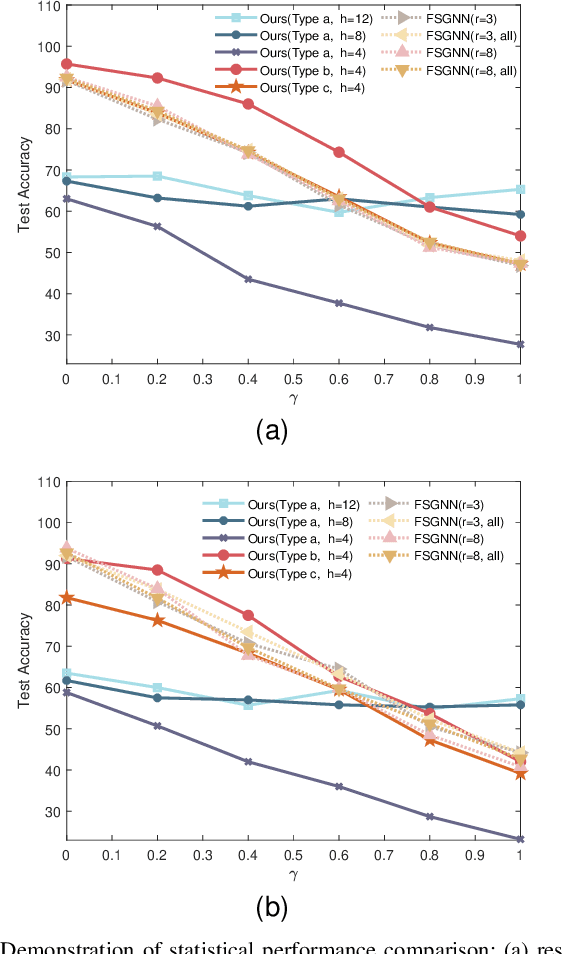
Abstract:The nature of heterophilous graphs is significantly different with that of homophilous graphs, which causes difficulties in early graph neural network models and suggests aggregations beyond 1-hop neighborhood. In this paper, we develop a new way to implement multi-scale extraction via constructing Haar-type graph framelets with desired properties of permutation equivariance, efficiency, and sparsity, for deep learning tasks on graphs. We further design a graph framelet neural network model PEGFAN (Permutation Equivariant Graph Framelet Augmented Network) based on our constructed graph framelets. The experiments are conducted on a synthetic dataset and 9 benchmark datasets to compare performance with other state-of-the-art models. The result shows that our model can achieve best performance on certain datasets of heterophilous graphs (including the majority of heterophilous datasets with relatively larger sizes and denser connections) and competitive performance on the remaining.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge