PHAT: Modeling Period Heterogeneity for Multivariate Time Series Forecasting

While existing multivariate time series forecasting models have advanced significantly in modeling periodicity, they largely neglect the periodic heterogeneity common in real-world data, where variates exhibit distinct and dynamically changing periods. To effectively capture this periodic heterogeneity, we propose PHAT (Period Heterogeneity-Aware Transformer). Specifically, PHAT arranges multivariate inputs into a three-dimensional "periodic bucket" tensor, where the dimensions correspond to variate group characteristics with similar periodicity, time steps aligned by phase, and offsets within the period. By restricting interactions within buckets and masking cross-bucket connections, PHAT effectively avoids interference from inconsistent periods. We also propose a positive-negative attention mechanism, which captures periodic dependencies from two perspectives: periodic alignment and periodic deviation. Additionally, the periodic alignment attention scores are decomposed into positive and negative components, with a modulation term encoding periodic priors. This modulation constrains the attention mechanism to more faithfully reflect the underlying periodic trends. A mathematical explanation is provided to support this property. We evaluate PHAT comprehensively on 14 real-world datasets against 18 baselines, and the results show that it significantly outperforms existing methods, achieving highly competitive forecasting performance. Our sources is available at GitHub.

To See Far, Look Close: Evolutionary Forecasting for Long-term Time Series

The prevailing Direct Forecasting (DF) paradigm dominates Long-term Time Series Forecasting (LTSF) by forcing models to predict the entire future horizon in a single forward pass. While efficient, this rigid coupling of output and evaluation horizons necessitates computationally prohibitive re-training for every target horizon. In this work, we uncover a counter-intuitive optimization anomaly: models trained on short horizons-when coupled with our proposed Evolutionary Forecasting (EF) paradigm-significantly outperform those trained directly on long horizons. We attribute this success to the mitigation of a fundamental optimization pathology inherent in DF, where conflicting gradients from distant futures cripple the learning of local dynamics. We establish EF as a unified generative framework, proving that DF is merely a degenerate special case of EF. Extensive experiments demonstrate that a singular EF model surpasses task-specific DF ensembles across standard benchmarks and exhibits robust asymptotic stability in extreme extrapolation. This work propels a paradigm shift in LTSF: moving from passive Static Mapping to autonomous Evolutionary Reasoning.

A General ReLearner: Empowering Spatiotemporal Prediction by Re-learning Input-label Residual

Prevailing spatiotemporal prediction models typically operate under a forward (unidirectional) learning paradigm, in which models extract spatiotemporal features from historical observation input and map them to target spatiotemporal space for future forecasting (label). However, these models frequently exhibit suboptimal performance when spatiotemporal discrepancies exist between inputs and labels, for instance, when nodes with similar time-series inputs manifest distinct future labels, or vice versa. To address this limitation, we propose explicitly incorporating label features during the training phase. Specifically, we introduce the Spatiotemporal Residual Theorem, which generalizes the conventional unidirectional spatiotemporal prediction paradigm into a bidirectional learning framework. Building upon this theoretical foundation, we design an universal module, termed ReLearner, which seamlessly augments Spatiotemporal Neural Networks (STNNs) with a bidirectional learning capability via an auxiliary inverse learning process. In this process, the model relearns the spatiotemporal feature residuals between input data and future data. The proposed ReLearner comprises two critical components: (1) a Residual Learning Module, designed to effectively disentangle spatiotemporal feature discrepancies between input and label representations; and (2) a Residual Smoothing Module, employed to smooth residual terms and facilitate stable convergence. Extensive experiments conducted on 11 real-world datasets across 14 backbone models demonstrate that ReLearner significantly enhances the predictive performance of existing STNNs.Our code is available on GitHub.

Spatiotemporal Causal Decoupling Model for Air Quality Forecasting

Due to the profound impact of air pollution on human health, livelihoods, and economic development, air quality forecasting is of paramount significance. Initially, we employ the causal graph method to scrutinize the constraints of existing research in comprehensively modeling the causal relationships between the air quality index (AQI) and meteorological features. In order to enhance prediction accuracy, we introduce a novel air quality forecasting model, AirCade, which incorporates a causal decoupling approach. AirCade leverages a spatiotemporal module in conjunction with knowledge embedding techniques to capture the internal dynamics of AQI. Subsequently, a causal decoupling module is proposed to disentangle synchronous causality from past AQI and meteorological features, followed by the dissemination of acquired knowledge to future time steps to enhance performance. Additionally, we introduce a causal intervention mechanism to explicitly represent the uncertainty of future meteorological features, thereby bolstering the model's robustness. Our evaluation of AirCade on an open-source air quality dataset demonstrates over 20\% relative improvement over state-of-the-art models.

Randomly Projected Convex Clustering Model: Motivation, Realization, and Cluster Recovery Guarantees

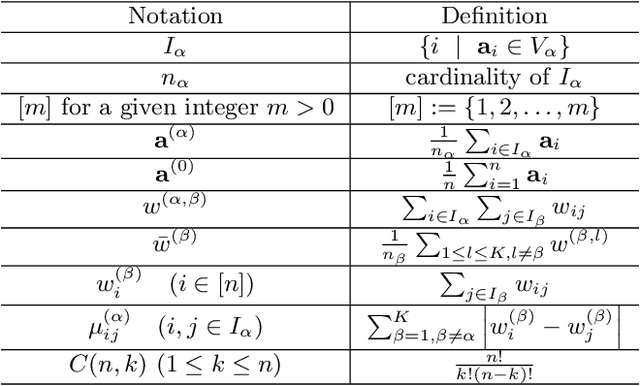
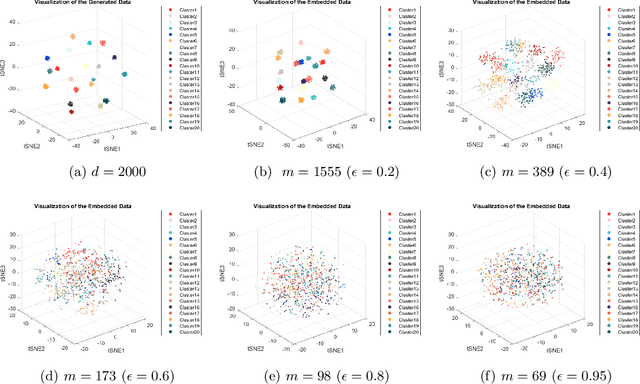
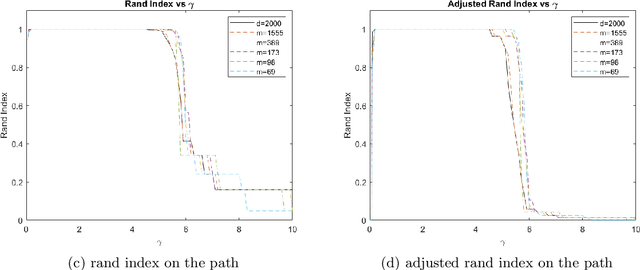
In this paper, we propose a randomly projected convex clustering model for clustering a collection of $n$ high dimensional data points in $\mathbb{R}^d$ with $K$ hidden clusters. Compared to the convex clustering model for clustering original data with dimension $d$, we prove that, under some mild conditions, the perfect recovery of the cluster membership assignments of the convex clustering model, if exists, can be preserved by the randomly projected convex clustering model with embedding dimension $m = O(\epsilon^{-2}\log(n))$, where $0 < \epsilon < 1$ is some given parameter. We further prove that the embedding dimension can be improved to be $O(\epsilon^{-2}\log(K))$, which is independent of the number of data points. Extensive numerical experiment results will be presented in this paper to demonstrate the robustness and superior performance of the randomly projected convex clustering model. The numerical results presented in this paper also demonstrate that the randomly projected convex clustering model can outperform the randomly projected K-means model in practice.