Randomly Projected Convex Clustering Model: Motivation, Realization, and Cluster Recovery Guarantees
Paper and Code
Mar 29, 2023
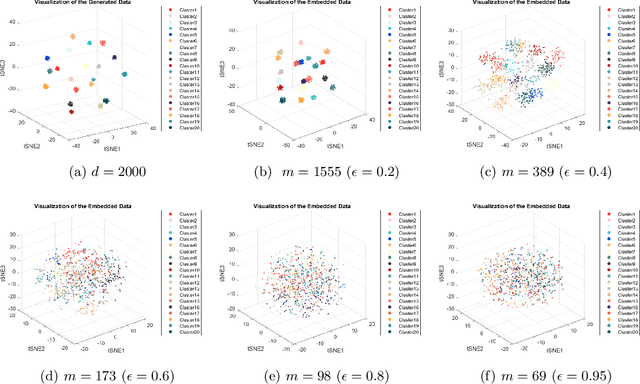

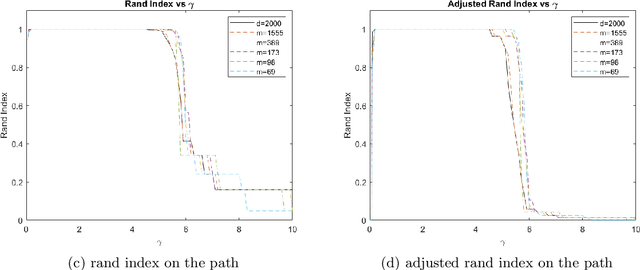
In this paper, we propose a randomly projected convex clustering model for clustering a collection of $n$ high dimensional data points in $\mathbb{R}^d$ with $K$ hidden clusters. Compared to the convex clustering model for clustering original data with dimension $d$, we prove that, under some mild conditions, the perfect recovery of the cluster membership assignments of the convex clustering model, if exists, can be preserved by the randomly projected convex clustering model with embedding dimension $m = O(\epsilon^{-2}\log(n))$, where $0 < \epsilon < 1$ is some given parameter. We further prove that the embedding dimension can be improved to be $O(\epsilon^{-2}\log(K))$, which is independent of the number of data points. Extensive numerical experiment results will be presented in this paper to demonstrate the robustness and superior performance of the randomly projected convex clustering model. The numerical results presented in this paper also demonstrate that the randomly projected convex clustering model can outperform the randomly projected K-means model in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge