Apollo-MILP: An Alternating Prediction-Correction Neural Solving Framework for Mixed-Integer Linear Programming

Leveraging machine learning (ML) to predict an initial solution for mixed-integer linear programming (MILP) has gained considerable popularity in recent years. These methods predict a solution and fix a subset of variables to reduce the problem dimension. Then, they solve the reduced problem to obtain the final solutions. However, directly fixing variable values can lead to low-quality solutions or even infeasible reduced problems if the predicted solution is not accurate enough. To address this challenge, we propose an Alternating prediction-correction neural solving framework (Apollo-MILP) that can identify and select accurate and reliable predicted values to fix. In each iteration, Apollo-MILP conducts a prediction step for the unfixed variables, followed by a correction step to obtain an improved solution (called reference solution) through a trust-region search. By incorporating the predicted and reference solutions, we introduce a novel Uncertainty-based Error upper BOund (UEBO) to evaluate the uncertainty of the predicted values and fix those with high confidence. A notable feature of Apollo-MILP is the superior ability for problem reduction while preserving optimality, leading to high-quality final solutions. Experiments on commonly used benchmarks demonstrate that our proposed Apollo-MILP significantly outperforms other ML-based approaches in terms of solution quality, achieving over a 50% reduction in the solution gap.

MILP-StuDio: MILP Instance Generation via Block Structure Decomposition

Mixed-integer linear programming (MILP) is one of the most popular mathematical formulations with numerous applications. In practice, improving the performance of MILP solvers often requires a large amount of high-quality data, which can be challenging to collect. Researchers thus turn to generation techniques to generate additional MILP instances. However, existing approaches do not take into account specific block structures -- which are closely related to the problem formulations -- in the constraint coefficient matrices (CCMs) of MILPs. Consequently, they are prone to generate computationally trivial or infeasible instances due to the disruptions of block structures and thus problem formulations. To address this challenge, we propose a novel MILP generation framework, called Block Structure Decomposition (MILP-StuDio), to generate high-quality instances by preserving the block structures. Specifically, MILP-StuDio begins by identifying the blocks in CCMs and decomposing the instances into block units, which serve as the building blocks of MILP instances. We then design three operators to construct new instances by removing, substituting, and appending block units in the original instances, enabling us to generate instances with flexible sizes. An appealing feature of MILP-StuDio is its strong ability to preserve the feasibility and computational hardness of the generated instances. Experiments on the commonly-used benchmarks demonstrate that using instances generated by MILP-StuDio is able to significantly reduce over 10% of the solving time for learning-based solvers.

Learning to Cut via Hierarchical Sequence/Set Model for Efficient Mixed-Integer Programming

Cutting planes (cuts) play an important role in solving mixed-integer linear programs (MILPs), which formulate many important real-world applications. Cut selection heavily depends on (P1) which cuts to prefer and (P2) how many cuts to select. Although modern MILP solvers tackle (P1)-(P2) by human-designed heuristics, machine learning carries the potential to learn more effective heuristics. However, many existing learning-based methods learn which cuts to prefer, neglecting the importance of learning how many cuts to select. Moreover, we observe that (P3) what order of selected cuts to prefer significantly impacts the efficiency of MILP solvers as well. To address these challenges, we propose a novel hierarchical sequence/set model (HEM) to learn cut selection policies. Specifically, HEM is a bi-level model: (1) a higher-level module that learns how many cuts to select, (2) and a lower-level module -- that formulates the cut selection as a sequence/set to sequence learning problem -- to learn policies selecting an ordered subset with the cardinality determined by the higher-level module. To the best of our knowledge, HEM is the first data-driven methodology that well tackles (P1)-(P3) simultaneously. Experiments demonstrate that HEM significantly improves the efficiency of solving MILPs on eleven challenging MILP benchmarks, including two Huawei's real problems.

Machine Learning Insides OptVerse AI Solver: Design Principles and Applications

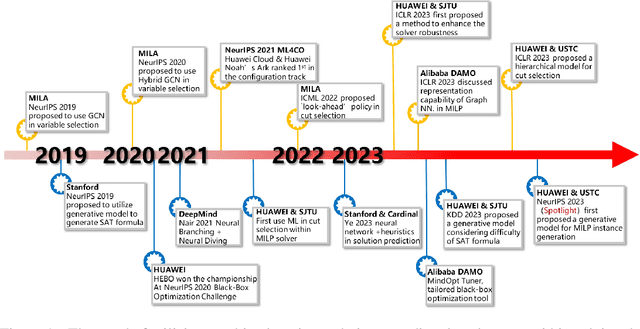
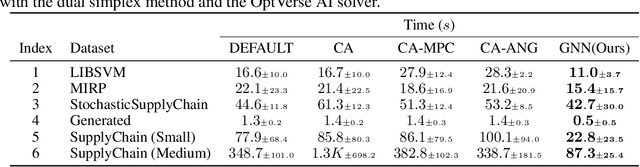
In an era of digital ubiquity, efficient resource management and decision-making are paramount across numerous industries. To this end, we present a comprehensive study on the integration of machine learning (ML) techniques into Huawei Cloud's OptVerse AI Solver, which aims to mitigate the scarcity of real-world mathematical programming instances, and to surpass the capabilities of traditional optimization techniques. We showcase our methods for generating complex SAT and MILP instances utilizing generative models that mirror multifaceted structures of real-world problem. Furthermore, we introduce a training framework leveraging augmentation policies to maintain solvers' utility in dynamic environments. Besides the data generation and augmentation, our proposed approaches also include novel ML-driven policies for personalized solver strategies, with an emphasis on applications like graph convolutional networks for initial basis selection and reinforcement learning for advanced presolving and cut selection. Additionally, we detail the incorporation of state-of-the-art parameter tuning algorithms which markedly elevate solver performance. Compared with traditional solvers such as Cplex and SCIP, our ML-augmented OptVerse AI Solver demonstrates superior speed and precision across both established benchmarks and real-world scenarios, reinforcing the practical imperative and effectiveness of machine learning techniques in mathematical programming solvers.

Promoting Generalization for Exact Solvers via Adversarial Instance Augmentation

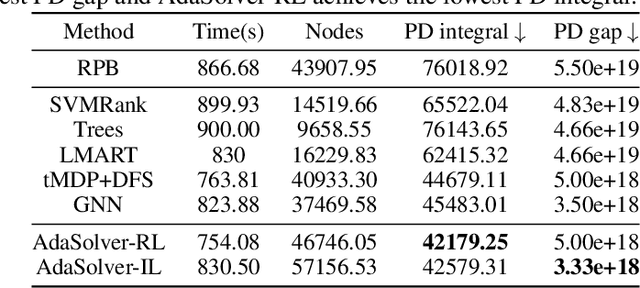
Machine learning has been successfully applied to improve the efficiency of Mixed-Integer Linear Programming (MILP) solvers. However, the learning-based solvers often suffer from severe performance degradation on unseen MILP instances -- especially on large-scale instances from a perturbed environment -- due to the limited diversity of training distributions. To tackle this problem, we propose a novel approach, which is called Adversarial Instance Augmentation and does not require to know the problem type for new instance generation, to promote data diversity for learning-based branching modules in the branch-and-bound (B&B) Solvers (AdaSolver). We use the bipartite graph representations for MILP instances and obtain various perturbed instances to regularize the solver by augmenting the graph structures with a learned augmentation policy. The major technical contribution of AdaSolver is that we formulate the non-differentiable instance augmentation as a contextual bandit problem and adversarially train the learning-based solver and augmentation policy, enabling efficient gradient-based training of the augmentation policy. To the best of our knowledge, AdaSolver is the first general and effective framework for understanding and improving the generalization of both imitation-learning-based (IL-based) and reinforcement-learning-based (RL-based) B&B solvers. Extensive experiments demonstrate that by producing various augmented instances, AdaSolver leads to a remarkable efficiency improvement across various distributions.

Accelerate Presolve in Large-Scale Linear Programming via Reinforcement Learning

Large-scale LP problems from industry usually contain much redundancy that severely hurts the efficiency and reliability of solving LPs, making presolve (i.e., the problem simplification module) one of the most critical components in modern LP solvers. However, how to design high-quality presolve routines -- that is, the program determining (P1) which presolvers to select, (P2) in what order to execute, and (P3) when to stop -- remains a highly challenging task due to the extensive requirements on expert knowledge and the large search space. Due to the sequential decision property of the task and the lack of expert demonstrations, we propose a simple and efficient reinforcement learning (RL) framework -- namely, reinforcement learning for presolve (RL4Presolve) -- to tackle (P1)-(P3) simultaneously. Specifically, we formulate the routine design task as a Markov decision process and propose an RL framework with adaptive action sequences to generate high-quality presolve routines efficiently. Note that adaptive action sequences help learn complex behaviors efficiently and adapt to various benchmarks. Experiments on two solvers (open-source and commercial) and eight benchmarks (real-world and synthetic) demonstrate that RL4Presolve significantly and consistently improves the efficiency of solving large-scale LPs, especially on benchmarks from industry. Furthermore, we optimize the hard-coded presolve routines in LP solvers by extracting rules from learned policies for simple and efficient deployment to Huawei's supply chain. The results show encouraging economic and academic potential for incorporating machine learning to modern solvers.

A Deep Instance Generative Framework for MILP Solvers Under Limited Data Availability

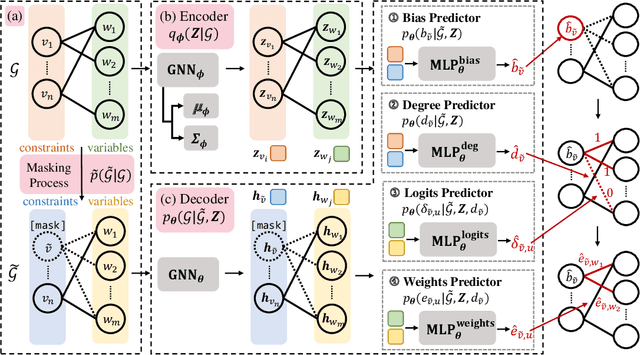
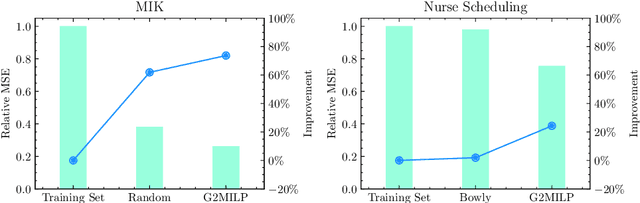
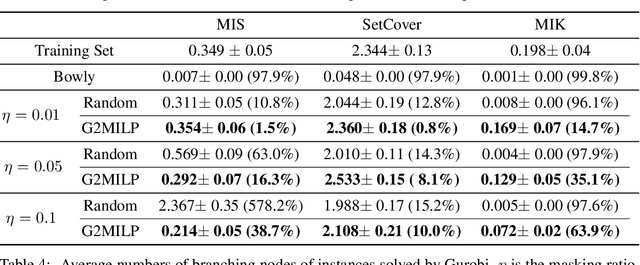
In the past few years, there has been an explosive surge in the use of machine learning (ML) techniques to address combinatorial optimization (CO) problems, especially mixed-integer linear programs (MILPs). Despite the achievements, the limited availability of real-world instances often leads to sub-optimal decisions and biased solver assessments, which motivates a suite of synthetic MILP instance generation techniques. However, existing methods either rely heavily on expert-designed formulations or struggle to capture the rich features of real-world instances. To tackle this problem, we propose G2MILP, which to the best of our knowledge is the first deep generative framework for MILP instances. Specifically, G2MILP represents MILP instances as bipartite graphs, and applies a masked variational autoencoder to iteratively corrupt and replace parts of the original graphs to generate new ones. The appealing feature of G2MILP is that it can learn to generate novel and realistic MILP instances without prior expert-designed formulations, while preserving the structures and computational hardness of real-world datasets, simultaneously. Thus the generated instances can facilitate downstream tasks for enhancing MILP solvers under limited data availability. We design a suite of benchmarks to evaluate the quality of the generated MILP instances. Experiments demonstrate that our method can produce instances that closely resemble real-world datasets in terms of both structures and computational hardness.

A Circuit Domain Generalization Framework for Efficient Logic Synthesis in Chip Design

Logic Synthesis (LS) plays a vital role in chip design -- a cornerstone of the semiconductor industry. A key task in LS is to transform circuits -- modeled by directed acyclic graphs (DAGs) -- into simplified circuits with equivalent functionalities. To tackle this task, many LS operators apply transformations to subgraphs -- rooted at each node on an input DAG -- sequentially. However, we found that a large number of transformations are ineffective, which makes applying these operators highly time-consuming. In particular, we notice that the runtime of the Resub and Mfs2 operators often dominates the overall runtime of LS optimization processes. To address this challenge, we propose a novel data-driven LS operator paradigm, namely PruneX, to reduce ineffective transformations. The major challenge of developing PruneX is to learn models that well generalize to unseen circuits, i.e., the out-of-distribution (OOD) generalization problem. Thus, the major technical contribution of PruneX is the novel circuit domain generalization framework, which learns domain-invariant representations based on the transformation-invariant domain-knowledge. To the best of our knowledge, PruneX is the first approach to tackle the OOD problem in LS operators. We integrate PruneX with the aforementioned Resub and Mfs2 operators. Experiments demonstrate that PruneX significantly improves their efficiency while keeping comparable optimization performance on industrial and very large-scale circuits, achieving up to $3.1\times$ faster runtime.

SGDP: A Stream-Graph Neural Network Based Data Prefetcher

Data prefetching is important for storage system optimization and access performance improvement. Traditional prefetchers work well for mining access patterns of sequential logical block address (LBA) but cannot handle complex non-sequential patterns that commonly exist in real-world applications. The state-of-the-art (SOTA) learning-based prefetchers cover more LBA accesses. However, they do not adequately consider the spatial interdependencies between LBA deltas, which leads to limited performance and robustness. This paper proposes a novel Stream-Graph neural network-based Data Prefetcher (SGDP). Specifically, SGDP models LBA delta streams using a weighted directed graph structure to represent interactive relations among LBA deltas and further extracts hybrid features by graph neural networks for data prefetching. We conduct extensive experiments on eight real-world datasets. Empirical results verify that SGDP outperforms the SOTA methods in terms of the hit ratio by 6.21%, the effective prefetching ratio by 7.00%, and speeds up inference time by 3.13X on average. Besides, we generalize SGDP to different variants by different stream constructions, further expanding its application scenarios and demonstrating its robustness. SGDP offers a novel data prefetching solution and has been verified in commercial hybrid storage systems in the experimental phase. Our codes and appendix are available at https://github.com/yyysjz1997/SGDP/.

HardSATGEN: Understanding the Difficulty of Hard SAT Formula Generation and A Strong Structure-Hardness-Aware Baseline

Industrial SAT formula generation is a critical yet challenging task for heuristic development and the surging learning-based methods in practical SAT applications. Existing SAT generation approaches can hardly simultaneously capture the global structural properties and maintain plausible computational hardness, which can be hazardous for the various downstream engagements. To this end, we first present an in-depth analysis for the limitation of previous learning methods in reproducing the computational hardness of original instances, which may stem from the inherent homogeneity in their adopted split-merge procedure. On top of the observations that industrial formulae exhibit clear community structure and oversplit substructures lead to the difficulty in semantic formation of logical structures, we propose HardSATGEN, which introduces a fine-grained control mechanism to the neural split-merge paradigm for SAT formula generation to better recover the structural and computational properties of the industrial benchmarks. Experimental results including evaluations on private corporate data and hyperparameter tuning over solvers in practical use show the significant superiority of HardSATGEN being the only method to successfully augments formulae maintaining similar computational hardness and capturing the global structural properties simultaneously. Compared to the best previous methods to our best knowledge, the average performance gains achieve 38.5% in structural statistics, 88.4% in computational metrics, and over 140.7% in the effectiveness of guiding solver development tuned by our generated instances.