SGDP: A Stream-Graph Neural Network Based Data Prefetcher

Data prefetching is important for storage system optimization and access performance improvement. Traditional prefetchers work well for mining access patterns of sequential logical block address (LBA) but cannot handle complex non-sequential patterns that commonly exist in real-world applications. The state-of-the-art (SOTA) learning-based prefetchers cover more LBA accesses. However, they do not adequately consider the spatial interdependencies between LBA deltas, which leads to limited performance and robustness. This paper proposes a novel Stream-Graph neural network-based Data Prefetcher (SGDP). Specifically, SGDP models LBA delta streams using a weighted directed graph structure to represent interactive relations among LBA deltas and further extracts hybrid features by graph neural networks for data prefetching. We conduct extensive experiments on eight real-world datasets. Empirical results verify that SGDP outperforms the SOTA methods in terms of the hit ratio by 6.21%, the effective prefetching ratio by 7.00%, and speeds up inference time by 3.13X on average. Besides, we generalize SGDP to different variants by different stream constructions, further expanding its application scenarios and demonstrating its robustness. SGDP offers a novel data prefetching solution and has been verified in commercial hybrid storage systems in the experimental phase. Our codes and appendix are available at https://github.com/yyysjz1997/SGDP/.

Block Hankel Tensor ARIMA for Multiple Short Time Series Forecasting

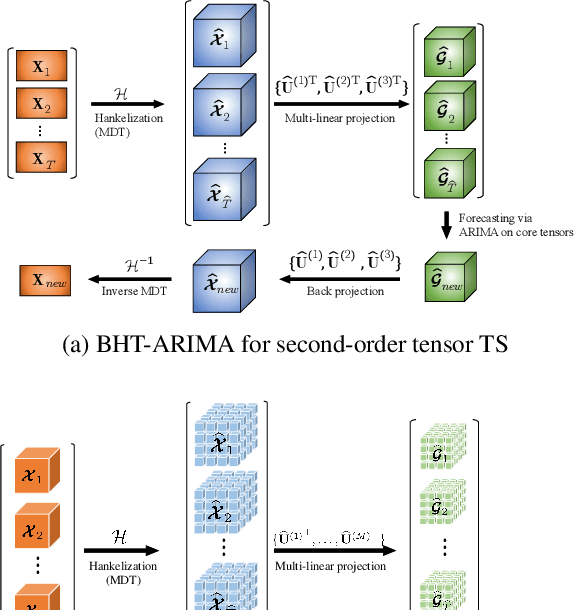
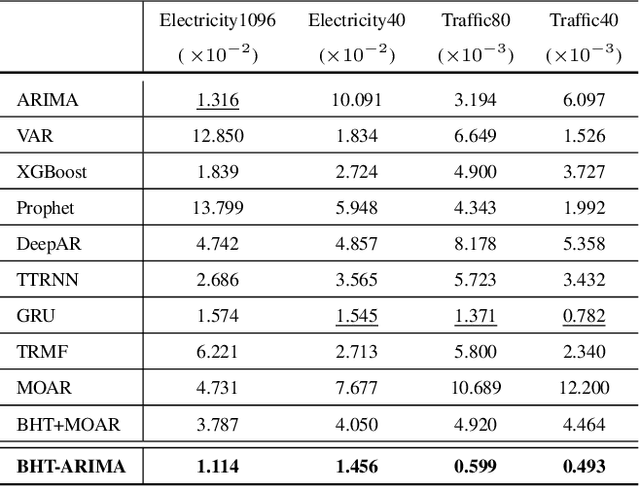
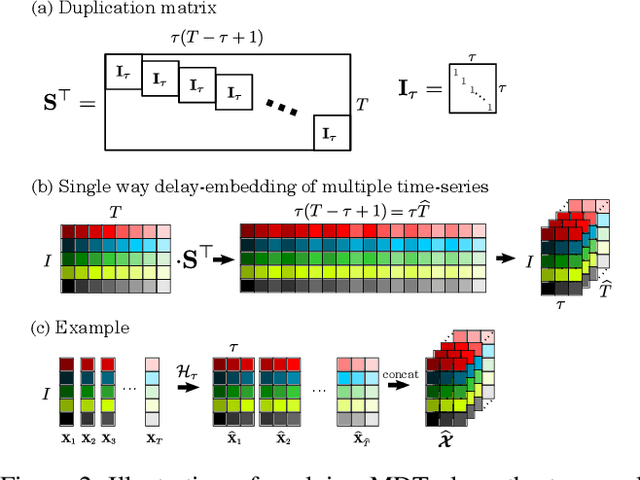
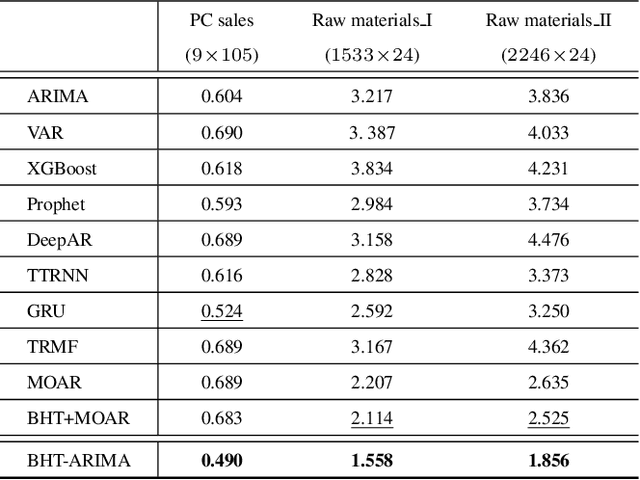
This work proposes a novel approach for multiple time series forecasting. At first, multi-way delay embedding transform (MDT) is employed to represent time series as low-rank block Hankel tensors (BHT). Then, the higher-order tensors are projected to compressed core tensors by applying Tucker decomposition. At the same time, the generalized tensor Autoregressive Integrated Moving Average (ARIMA) is explicitly used on consecutive core tensors to predict future samples. In this manner, the proposed approach tactically incorporates the unique advantages of MDT tensorization (to exploit mutual correlations) and tensor ARIMA coupled with low-rank Tucker decomposition into a unified framework. This framework exploits the low-rank structure of block Hankel tensors in the embedded space and captures the intrinsic correlations among multiple TS, which thus can improve the forecasting results, especially for multiple short time series. Experiments conducted on three public datasets and two industrial datasets verify that the proposed BHT-ARIMA effectively improves forecasting accuracy and reduces computational cost compared with the state-of-the-art methods.

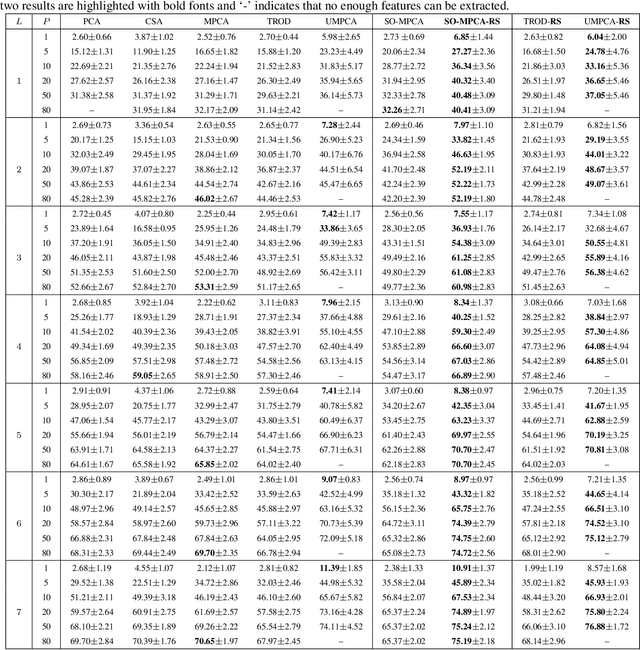
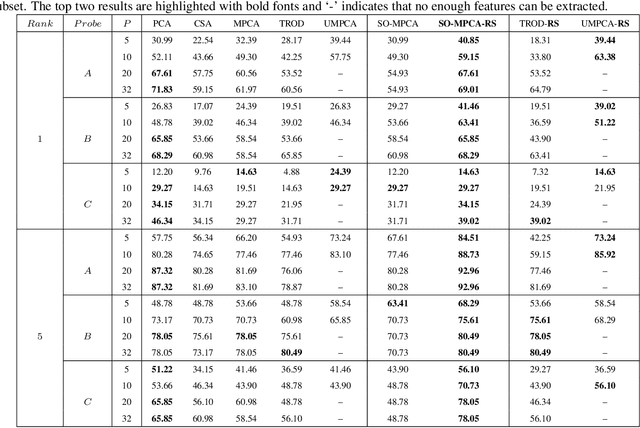
Semi-Orthogonal Multilinear PCA with Relaxed Start

Principal component analysis (PCA) is an unsupervised method for learning low-dimensional features with orthogonal projections. Multilinear PCA methods extend PCA to deal with multidimensional data (tensors) directly via tensor-to-tensor projection or tensor-to-vector projection (TVP). However, under the TVP setting, it is difficult to develop an effective multilinear PCA method with the orthogonality constraint. This paper tackles this problem by proposing a novel Semi-Orthogonal Multilinear PCA (SO-MPCA) approach. SO-MPCA learns low-dimensional features directly from tensors via TVP by imposing the orthogonality constraint in only one mode. This formulation results in more captured variance and more learned features than full orthogonality. For better generalization, we further introduce a relaxed start (RS) strategy to get SO-MPCA-RS by fixing the starting projection vectors, which increases the bias and reduces the variance of the learning model. Experiments on both face (2D) and gait (3D) data demonstrate that SO-MPCA-RS outperforms other competing algorithms on the whole, and the relaxed start strategy is also effective for other TVP-based PCA methods.