Very Basics of Tensors with Graphical Notations: Unfolding, Calculations, and Decompositions

Tensor network diagram (graphical notation) is a useful tool that graphically represents multiplications between multiple tensors using nodes and edges. Using the graphical notation, complex multiplications between tensors can be described simply and intuitively, and it also helps to understand the essence of tensor products. In fact, most of matrix/tensor products including inner product, outer product, Hadamard product, Kronecker product, and Khatri-Rao product can be written in graphical notation. These matrix/tensor operations are essential building blocks for the use of matrix/tensor decompositions in signal processing and machine learning. The purpose of this lecture note is to learn the very basics of tensors and how to represent them in mathematical symbols and graphical notation. Many papers using tensors omit these detailed definitions and explanations, which can be difficult for the reader. I hope this note will be of help to such readers.

Broadcast Product: Shape-aligned Element-wise Multiplication and Beyond

We propose a new operator defined between two tensors, the broadcast product. The broadcast product calculates the Hadamard product after duplicating elements to align the shapes of the two tensors. Complex tensor operations in libraries like \texttt{numpy} can be succinctly represented as mathematical expressions using the broadcast product. Finally, we propose a novel tensor decomposition using the broadcast product, highlighting its potential applications in dimensionality reduction.

Adaptive Block Sparse Regularization under Arbitrary Linear Transform

We propose a convex signal reconstruction method for block sparsity under arbitrary linear transform with unknown block structure. The proposed method is a generalization of the existing method LOP-$\ell_2$/$\ell_1$ and can reconstruct signals with block sparsity under non-invertible transforms, unlike LOP-$\ell_2$/$\ell_1$. Our work broadens the scope of block sparse regularization, enabling more versatile and powerful applications across various signal processing domains. We derive an iterative algorithm for solving proposed method and provide conditions for its convergence to the optimal solution. Numerical experiments demonstrate the effectiveness of the proposed method.

ADMM-MM Algorithm for General Tensor Decomposition

In this paper, we propose a new unified optimization algorithm for general tensor decomposition which is formulated as an inverse problem for low-rank tensors in the general linear observation models. The proposed algorithm supports three basic loss functions ($\ell_2$-loss, $\ell_1$-loss and KL divergence) and various low-rank tensor decomposition models (CP, Tucker, TT, and TR decompositions). We derive the optimization algorithm based on hierarchical combination of the alternating direction method of multiplier (ADMM) and majorization-minimization (MM). We show that wide-range applications can be solved by the proposed algorithm, and can be easily extended to any established tensor decomposition models in a {plug-and-play} manner.

Soft Smoothness for Audio Inpainting Using a Latent Matrix Model in Delay-embedded Space

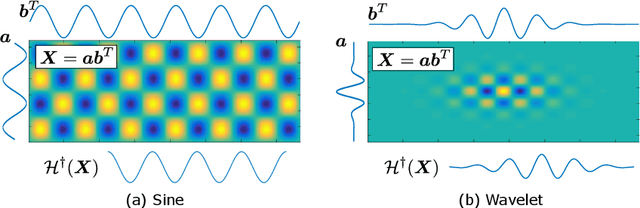
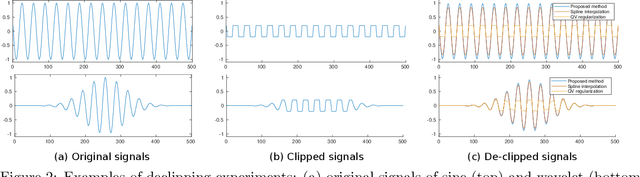
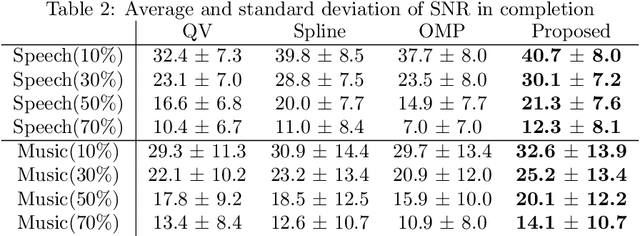
Here, we propose a new reconstruction method of smooth time-series signals. A key concept of this study is not considering the model in signal space, but in delay-embedded space. In other words, we indirectly represent a time-series signal as an output of inverse delay-embedding of a matrix, and the matrix is constrained. Based on the model under inverse delay-embedding, we propose to constrain the matrix to be rank-1 with smooth factor vectors. The proposed model is closely related to the convolutional model, and quadratic variation (QV) regularization. Especially, the proposed method can be characterized as a generalization of QV regularization. In addition, we show that the proposed method provides the softer smoothness than QV regularization. Experiments of audio inpainting and declipping are conducted to show its advantages in comparison with several existing interpolation methods and sparse modeling.

Manifold Modeling in Quotient Space: Learning An Invariant Mapping with Decodability of Image Patches

This study proposes a framework for manifold learning of image patches using the concept of equivalence classes: manifold modeling in quotient space (MMQS). In MMQS, we do not consider a set of local patches of the image as it is, but rather the set of their canonical patches obtained by introducing the concept of equivalence classes and performing manifold learning on their canonical patches. Canonical patches represent equivalence classes, and their auto-encoder constructs a manifold in the quotient space. Based on this framework, we produce a novel manifold-based image model by introducing rotation-flip-equivalence relations. In addition, we formulate an image reconstruction problem by fitting the proposed image model to a corrupted observed image and derive an algorithm to solve it. Our experiments show that the proposed image model is effective for various self-supervised image reconstruction tasks, such as image inpainting, deblurring, super-resolution, and denoising.

Block Hankel Tensor ARIMA for Multiple Short Time Series Forecasting

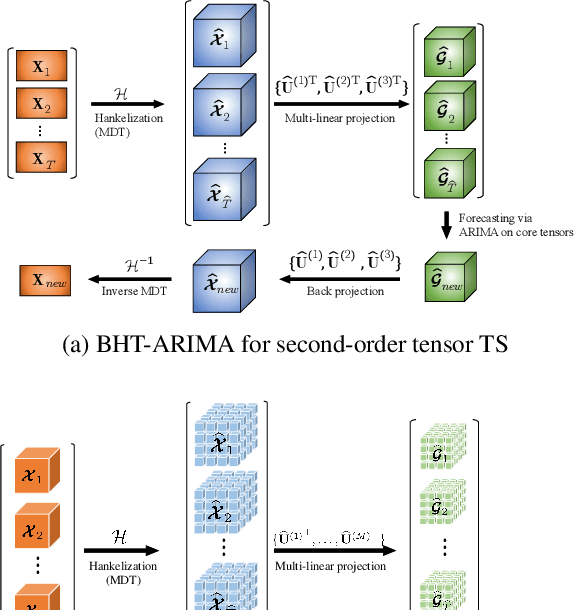
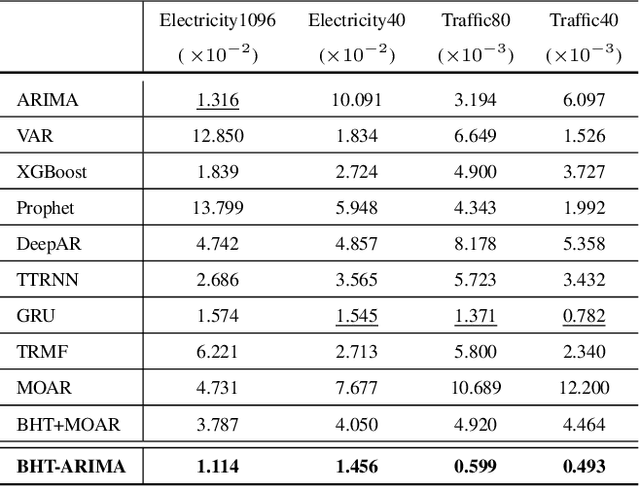
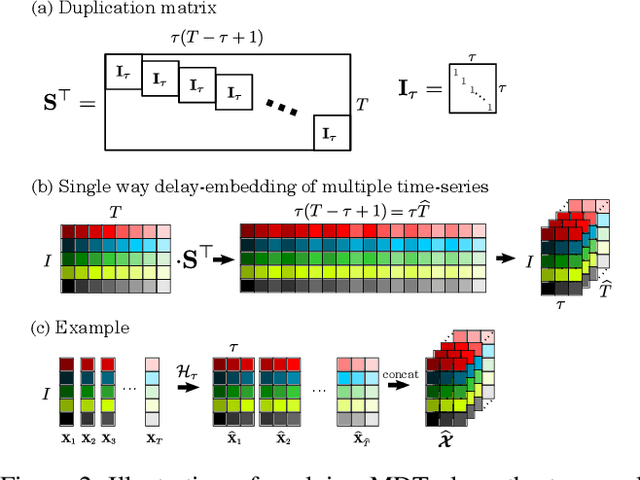
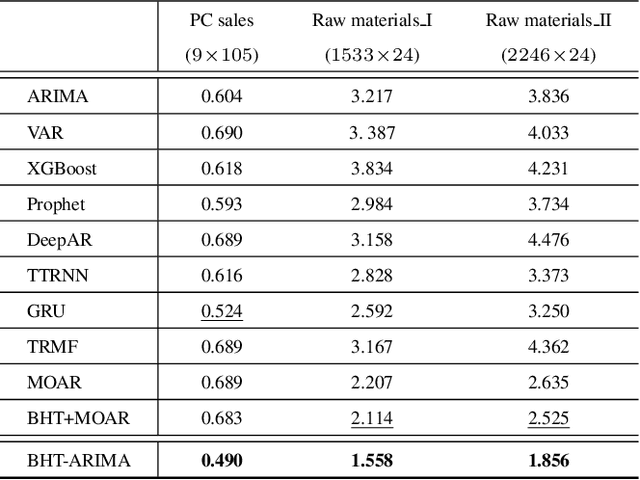
This work proposes a novel approach for multiple time series forecasting. At first, multi-way delay embedding transform (MDT) is employed to represent time series as low-rank block Hankel tensors (BHT). Then, the higher-order tensors are projected to compressed core tensors by applying Tucker decomposition. At the same time, the generalized tensor Autoregressive Integrated Moving Average (ARIMA) is explicitly used on consecutive core tensors to predict future samples. In this manner, the proposed approach tactically incorporates the unique advantages of MDT tensorization (to exploit mutual correlations) and tensor ARIMA coupled with low-rank Tucker decomposition into a unified framework. This framework exploits the low-rank structure of block Hankel tensors in the embedded space and captures the intrinsic correlations among multiple TS, which thus can improve the forecasting results, especially for multiple short time series. Experiments conducted on three public datasets and two industrial datasets verify that the proposed BHT-ARIMA effectively improves forecasting accuracy and reduces computational cost compared with the state-of-the-art methods.

Manifold Modeling in Embedded Space: A Perspective for Interpreting "Deep Image Prior"

Deep image prior (DIP), which utilizes a deep convolutional network (ConvNet) structure itself as an image prior, has attractive attentions in computer vision community. It empirically showed that the effectiveness of ConvNet structure in various image restoration applications. However, why the DIP works so well is still in black box, and why ConvNet is essential for images is not very clear. In this study, we tackle this question by considering the convolution divided into "embedding" and "transformation", and proposing a simple, but essential, modeling approach of images/tensors related with dynamical system or self-similarity. The proposed approach named as manifold modeling in embedded space (MMES) can be implemented by using a denoising-auto-encoder in combination with multiway delay-embedding transform. In spite of its simplicity, the image/tensor completion and super-resolution results of MMES were very similar even competitive with DIP in our experiments, and these results would help us for reinterpreting/characterizing the DIP from a perspective of "smooth patch-manifold prior".

Missing Slice Recovery for Tensors Using a Low-rank Model in Embedded Space

Let us consider a case where all of the elements in some continuous slices are missing in tensor data. In this case, the nuclear-norm and total variation regularization methods usually fail to recover the missing elements. The key problem is capturing some delay/shift-invariant structure. In this study, we consider a low-rank model in an embedded space of a tensor. For this purpose, we extend a delay embedding for a time series to a "multi-way delay-embedding transform" for a tensor, which takes a given incomplete tensor as the input and outputs a higher-order incomplete Hankel tensor. The higher-order tensor is then recovered by Tucker-based low-rank tensor factorization. Finally, an estimated tensor can be obtained by using the inverse multi-way delay embedding transform of the recovered higher-order tensor. Our experiments showed that the proposed method successfully recovered missing slices for some color images and functional magnetic resonance images.

Simultaneous Tensor Completion and Denoising by Noise Inequality Constrained Convex Optimization

Tensor completion is a technique of filling missing elements of the incomplete data tensors. It being actively studied based on the convex optimization scheme such as nuclear-norm minimization. When given data tensors include some noises, the nuclear-norm minimization problem is usually converted to the nuclear-norm `regularization' problem which simultaneously minimize penalty and error terms with some trade-off parameter. However, the good value of trade-off is not easily determined because of the difference of two units and the data dependence. In the sense of trade-off tuning, the noisy tensor completion problem with the `noise inequality constraint' is better choice than the `regularization' because the good noise threshold can be easily bounded with noise standard deviation. In this study, we tackle to solve the convex tensor completion problems with two types of noise inequality constraints: Gaussian and Laplace distributions. The contributions of this study are follows: (1) New tensor completion and denoising models using tensor total variation and nuclear-norm are proposed which can be characterized as a generalization/extension of many past matrix and tensor completion models, (2) proximal mappings for noise inequalities are derived which are analytically computable with low computational complexity, (3) convex optimization algorithm is proposed based on primal-dual splitting framework, (4) new step-size adaptation method is proposed to accelerate the optimization, and (5) extensive experiments demonstrated the advantages of the proposed method for visual data retrieval such as for color images, movies, and 3D-volumetric data.