WEEP: A Differentiable Nonconvex Sparse Regularizer via Weakly-Convex Envelope

Sparse regularization is fundamental in signal processing for efficient signal recovery and feature extraction. However, it faces a fundamental dilemma: the most powerful sparsity-inducing penalties are often non-differentiable, conflicting with gradient-based optimizers that dominate the field. We introduce WEEP (Weakly-convex Envelope of Piecewise Penalty), a novel, fully differentiable sparse regularizer derived from the weakly-convex envelope framework. WEEP provides strong, unbiased sparsity while maintaining full differentiability and L-smoothness, making it natively compatible with any gradient-based optimizer. This resolves the conflict between statistical performance and computational tractability. We demonstrate superior performance compared to the L1-norm and other established non-convex sparse regularizers on challenging signal and image denoising tasks.

Explainable Classifier for Malignant Lymphoma Subtyping via Cell Graph and Image Fusion

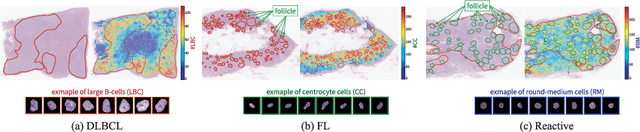
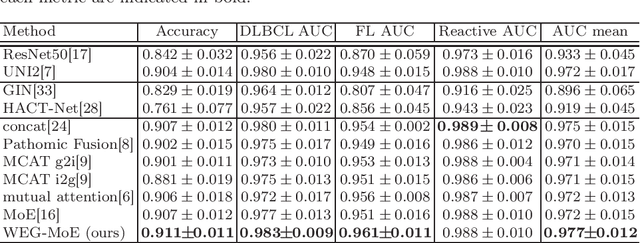
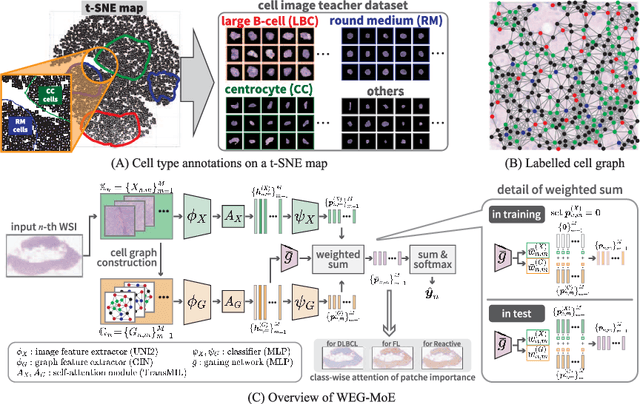
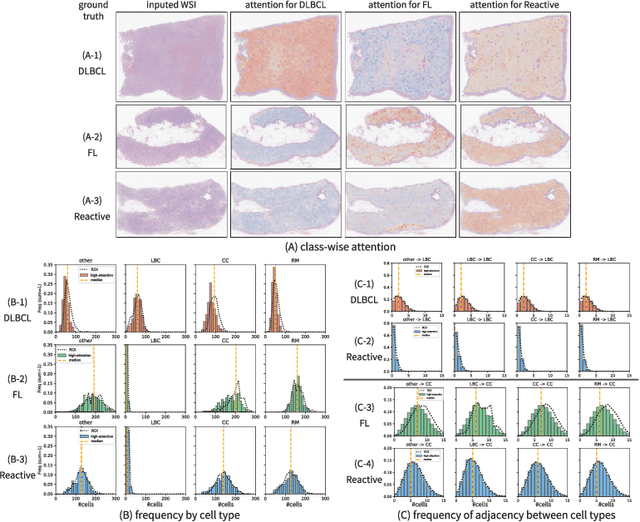
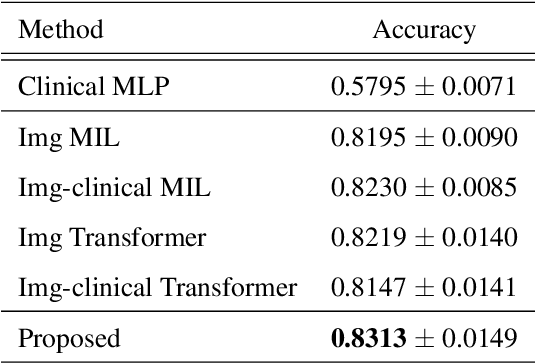
Malignant lymphoma subtype classification directly impacts treatment strategies and patient outcomes, necessitating classification models that achieve both high accuracy and sufficient explainability. This study proposes a novel explainable Multi-Instance Learning (MIL) framework that identifies subtype-specific Regions of Interest (ROIs) from Whole Slide Images (WSIs) while integrating cell distribution characteristics and image information. Our framework simultaneously addresses three objectives: (1) indicating appropriate ROIs for each subtype, (2) explaining the frequency and spatial distribution of characteristic cell types, and (3) achieving high-accuracy subtyping by leveraging both image and cell-distribution modalities. The proposed method fuses cell graph and image features extracted from each patch in the WSI using a Mixture-of-Experts (MoE) approach and classifies subtypes within an MIL framework. Experiments on a dataset of 1,233 WSIs demonstrate that our approach achieves state-of-the-art accuracy among ten comparative methods and provides region-level and cell-level explanations that align with a pathologist's perspectives.

Adaptive Block Sparse Regularization under Arbitrary Linear Transform

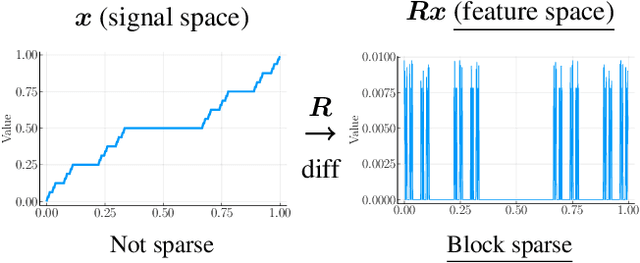
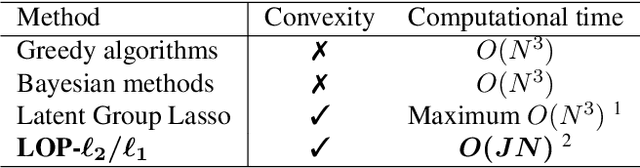
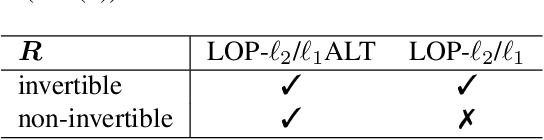
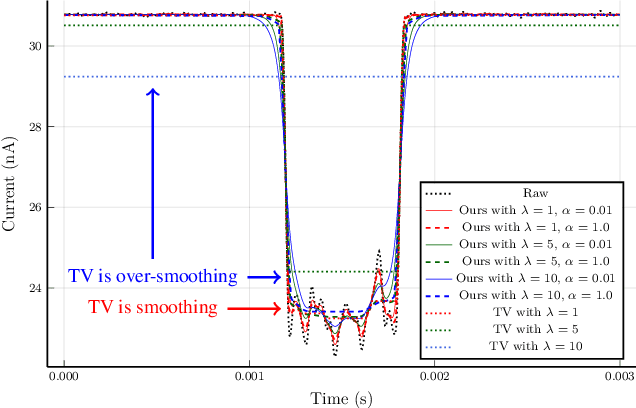
We propose a convex signal reconstruction method for block sparsity under arbitrary linear transform with unknown block structure. The proposed method is a generalization of the existing method LOP-$\ell_2$/$\ell_1$ and can reconstruct signals with block sparsity under non-invertible transforms, unlike LOP-$\ell_2$/$\ell_1$. Our work broadens the scope of block sparse regularization, enabling more versatile and powerful applications across various signal processing domains. We derive an iterative algorithm for solving proposed method and provide conditions for its convergence to the optimal solution. Numerical experiments demonstrate the effectiveness of the proposed method.

ADMM-MM Algorithm for General Tensor Decomposition

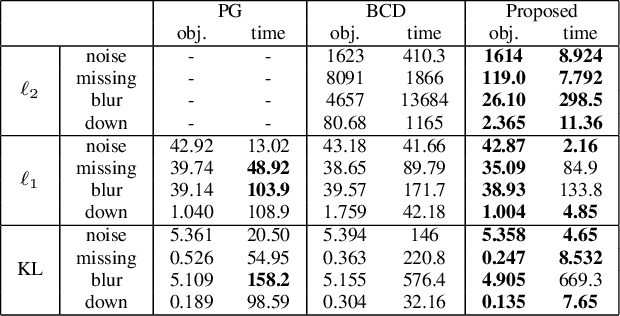
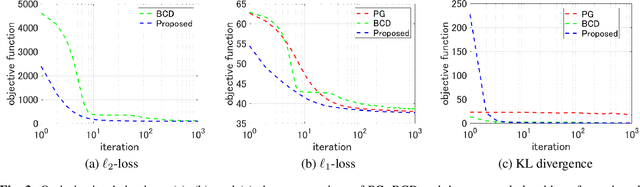
In this paper, we propose a new unified optimization algorithm for general tensor decomposition which is formulated as an inverse problem for low-rank tensors in the general linear observation models. The proposed algorithm supports three basic loss functions ($\ell_2$-loss, $\ell_1$-loss and KL divergence) and various low-rank tensor decomposition models (CP, Tucker, TT, and TR decompositions). We derive the optimization algorithm based on hierarchical combination of the alternating direction method of multiplier (ADMM) and majorization-minimization (MM). We show that wide-range applications can be solved by the proposed algorithm, and can be easily extended to any established tensor decomposition models in a {plug-and-play} manner.

Transformer-based Personalized Attention Mechanism (PersAM) for Medical Images with Clinical Records

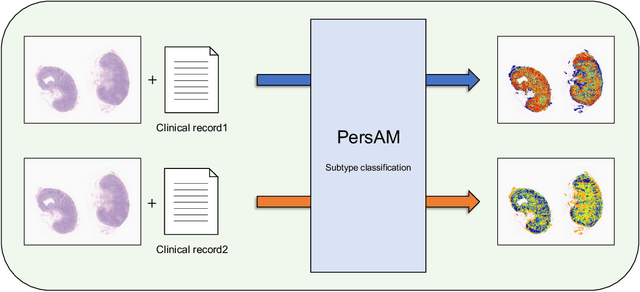
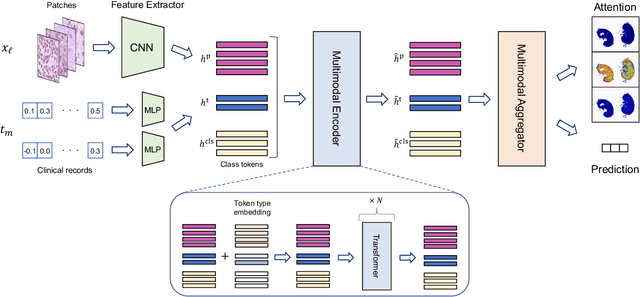
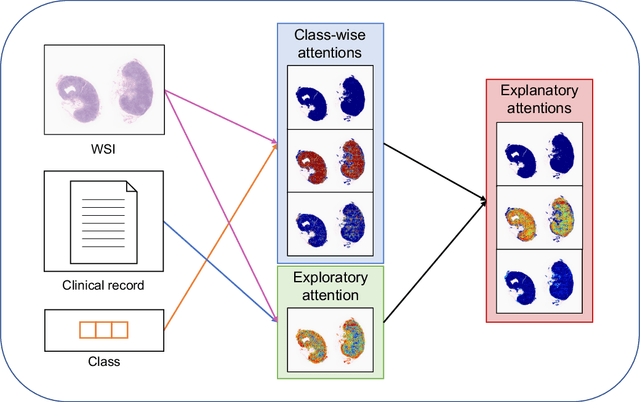
In medical image diagnosis, identifying the attention region, i.e., the region of interest for which the diagnosis is made, is an important task. Various methods have been developed to automatically identify target regions from given medical images. However, in actual medical practice, the diagnosis is made based not only on the images but also on a variety of clinical records. This means that pathologists examine medical images with some prior knowledge of the patients and that the attention regions may change depending on the clinical records. In this study, we propose a method called the Personalized Attention Mechanism (PersAM), by which the attention regions in medical images are adaptively changed according to the clinical records. The primary idea of the PersAM method is to encode the relationships between the medical images and clinical records using a variant of Transformer architecture. To demonstrate the effectiveness of the PersAM method, we applied it to a large-scale digital pathology problem of identifying the subtypes of 842 malignant lymphoma patients based on their gigapixel whole slide images and clinical records.

Manifold Modeling in Quotient Space: Learning An Invariant Mapping with Decodability of Image Patches

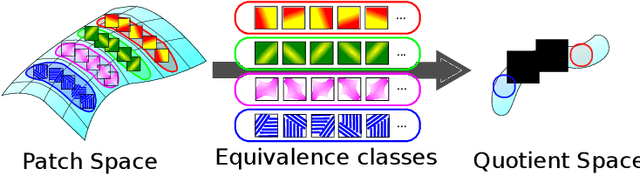
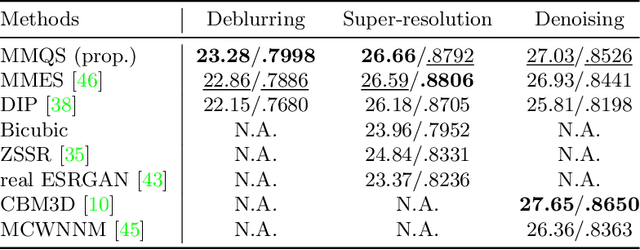
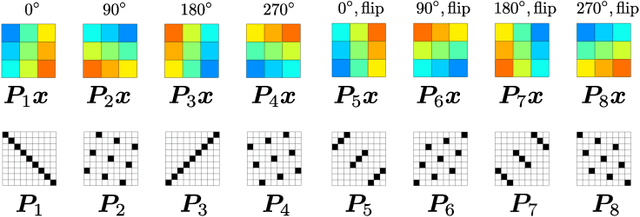
This study proposes a framework for manifold learning of image patches using the concept of equivalence classes: manifold modeling in quotient space (MMQS). In MMQS, we do not consider a set of local patches of the image as it is, but rather the set of their canonical patches obtained by introducing the concept of equivalence classes and performing manifold learning on their canonical patches. Canonical patches represent equivalence classes, and their auto-encoder constructs a manifold in the quotient space. Based on this framework, we produce a novel manifold-based image model by introducing rotation-flip-equivalence relations. In addition, we formulate an image reconstruction problem by fitting the proposed image model to a corrupted observed image and derive an algorithm to solve it. Our experiments show that the proposed image model is effective for various self-supervised image reconstruction tasks, such as image inpainting, deblurring, super-resolution, and denoising.

Case-based similar image retrieval for weakly annotated large histopathological images of malignant lymphoma using deep metric learning

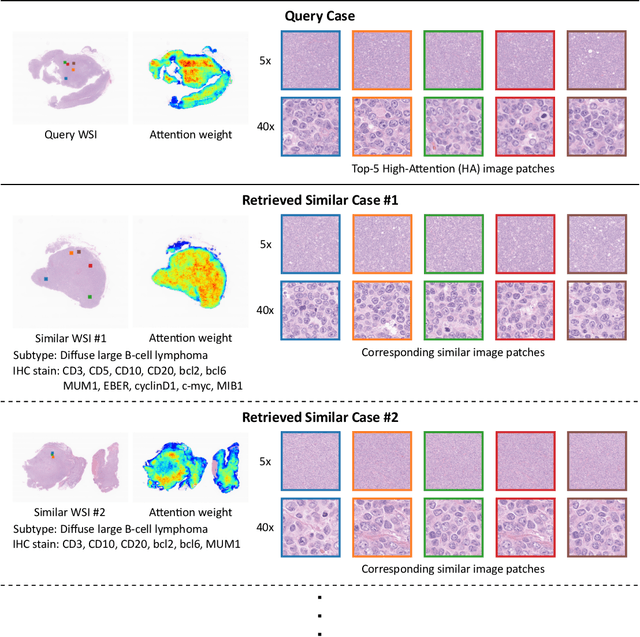
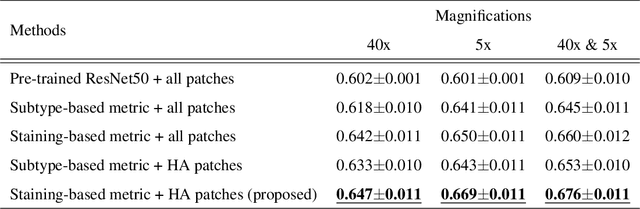
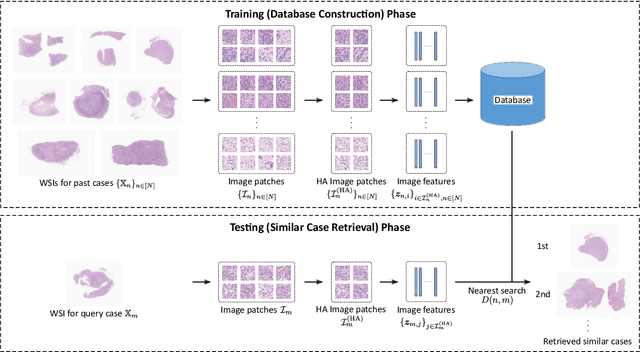
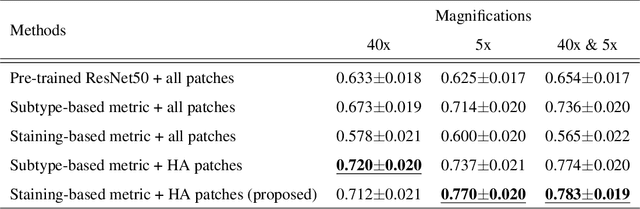
In the present study, we propose a novel case-based similar image retrieval (SIR) method for hematoxylin and eosin (H&E)-stained histopathological images of malignant lymphoma. When a whole slide image (WSI) is used as an input query, it is desirable to be able to retrieve similar cases by focusing on image patches in pathologically important regions such as tumor cells. To address this problem, we employ attention-based multiple instance learning, which enables us to focus on tumor-specific regions when the similarity between cases is computed. Moreover, we employ contrastive distance metric learning to incorporate immunohistochemical (IHC) staining patterns as useful supervised information for defining appropriate similarity between heterogeneous malignant lymphoma cases. In the experiment with 249 malignant lymphoma patients, we confirmed that the proposed method exhibited higher evaluation measures than the baseline case-based SIR methods. Furthermore, the subjective evaluation by pathologists revealed that our similarity measure using IHC staining patterns is appropriate for representing the similarity of H&E-stained tissue images for malignant lymphoma.

Multi-scale domain-adversarial multiple-instance CNN for cancer subtype classification with non-annotated histopathological images

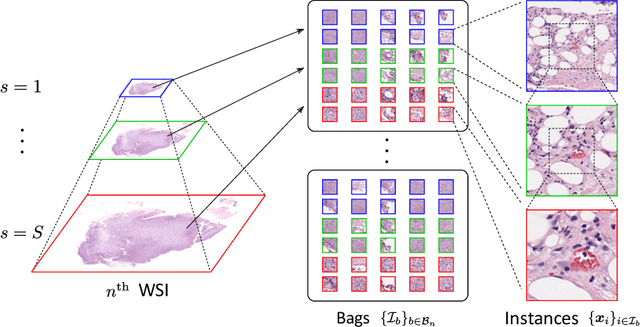
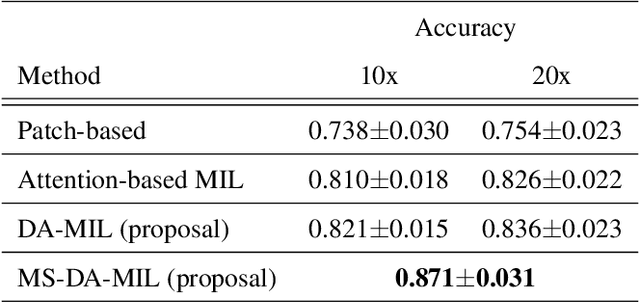
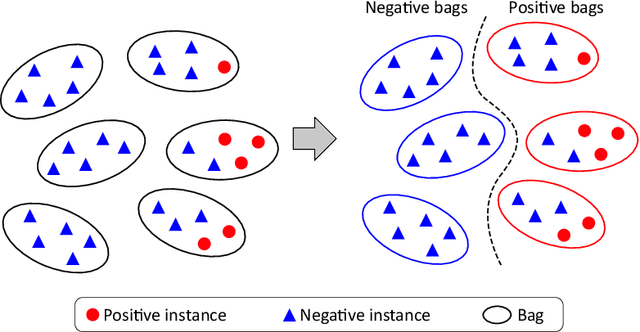
We propose a new method for cancer subtype classification from histopathological images, which can automatically detect tumor-specific features in a given whole slide image (WSI). The cancer subtype should be classified by referring to a WSI, i.e., a large size image (typically 40,000x40,000 pixels) of an entire pathological tissue slide, which consists of cancer and non-cancer portions. One difficulty for constructing cancer subtype classifiers comes from the high cost needed for annotating WSIs; without annotation, we have to construct the tumor region detector without knowing true labels. Furthermore, both global and local image features must be extracted from the WSI by changing the magnifications of the image. In addition, the image features should be stably detected against the variety/difference of staining among the hospitals/specimen. In this paper, we develop a new CNN-based cancer subtype classification method by effectively combining multiple-instance, domain adversarial, and multi-scale learning frameworks that can overcome these practical difficulties. When the proposed method was applied to malignant lymphoma subtype classifications of 196 cases collected from multiple hospitals, the classification performance was significantly better than the standard CNN or other conventional methods, and the accuracy was favorably compared to that of standard pathologists. In addition, we confirmed by immunostaining and expert pathologist's visual inspections that the tumor regions were correctly detected.

Manifold Modeling in Embedded Space: A Perspective for Interpreting "Deep Image Prior"

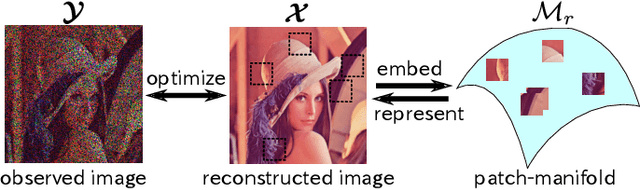
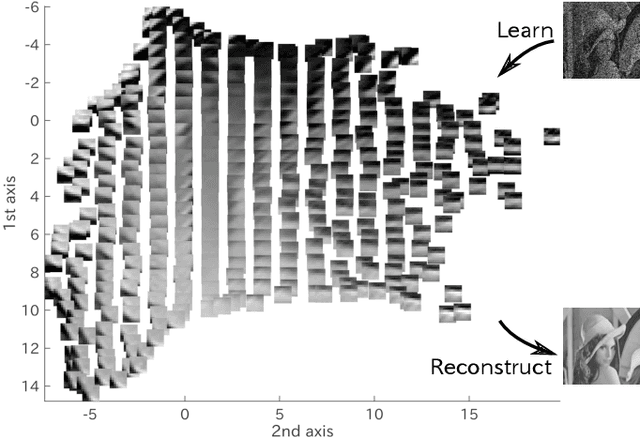
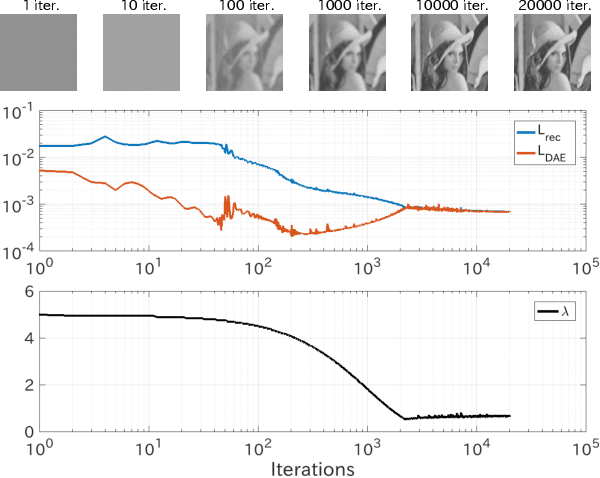
Deep image prior (DIP), which utilizes a deep convolutional network (ConvNet) structure itself as an image prior, has attractive attentions in computer vision community. It empirically showed that the effectiveness of ConvNet structure in various image restoration applications. However, why the DIP works so well is still in black box, and why ConvNet is essential for images is not very clear. In this study, we tackle this question by considering the convolution divided into "embedding" and "transformation", and proposing a simple, but essential, modeling approach of images/tensors related with dynamical system or self-similarity. The proposed approach named as manifold modeling in embedded space (MMES) can be implemented by using a denoising-auto-encoder in combination with multiway delay-embedding transform. In spite of its simplicity, the image/tensor completion and super-resolution results of MMES were very similar even competitive with DIP in our experiments, and these results would help us for reinterpreting/characterizing the DIP from a perspective of "smooth patch-manifold prior".

Computing Valid p-values for Image Segmentation by Selective Inference

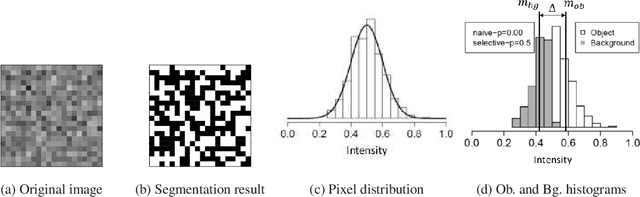
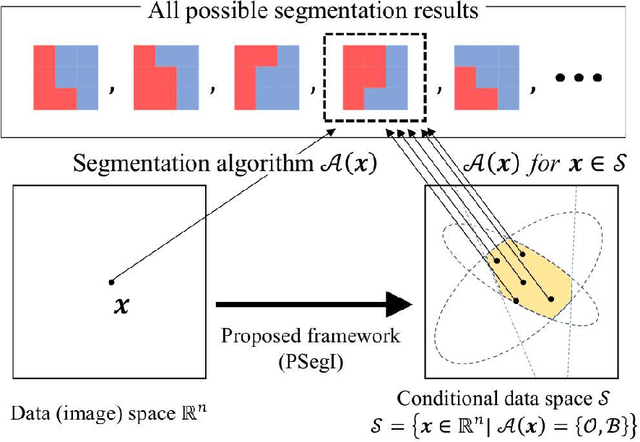
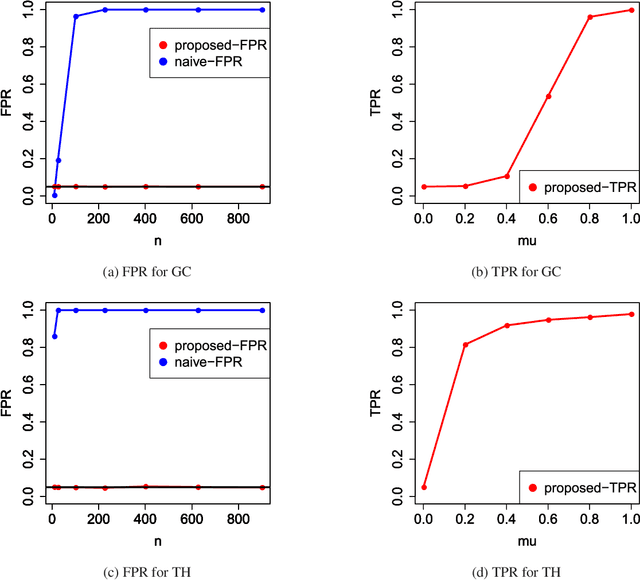
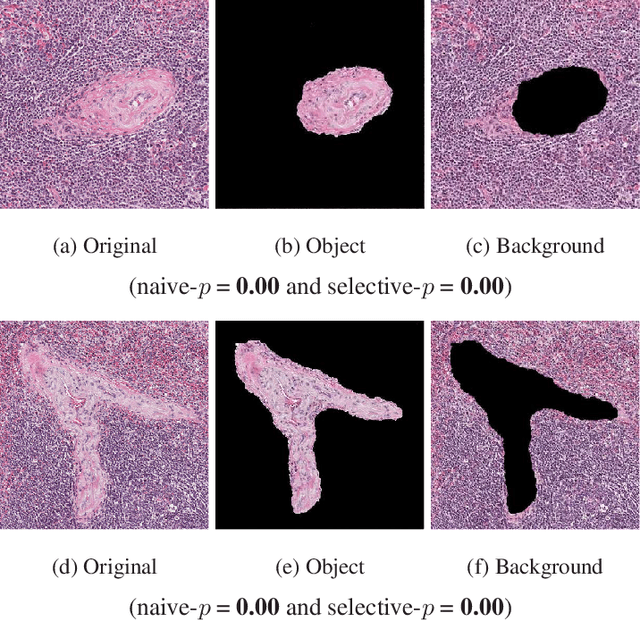
Image segmentation is one of the most fundamental tasks of computer vision. In many practical applications, it is essential to properly evaluate the reliability of individual segmentation results. In this study, we propose a novel framework to provide the statistical significance of segmentation results in the form of p-values. Specifically, we consider a statistical hypothesis test for determining the difference between the object and the background regions. This problem is challenging because the difference can be deceptively large (called segmentation bias) due to the adaptation of the segmentation algorithm to the data. To overcome this difficulty, we introduce a statistical approach called selective inference, and develop a framework to compute valid p-values in which the segmentation bias is properly accounted for. Although the proposed framework is potentially applicable to various segmentation algorithms, we focus in this paper on graph cut-based and threshold-based segmentation algorithms, and develop two specific methods to compute valid p-values for the segmentation results obtained by these algorithms. We prove the theoretical validity of these two methods and demonstrate their practicality by applying them to segmentation problems for medical images.