Manabu Mukai
ADMM-MM Algorithm for General Tensor Decomposition
Dec 19, 2023
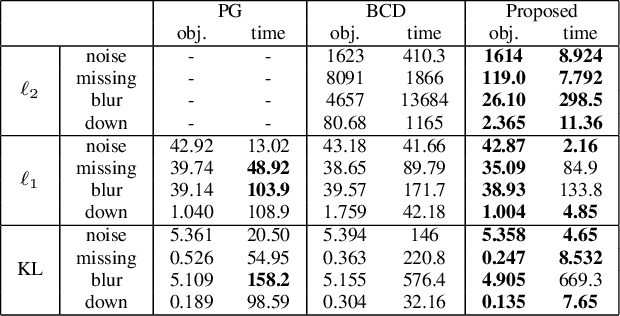
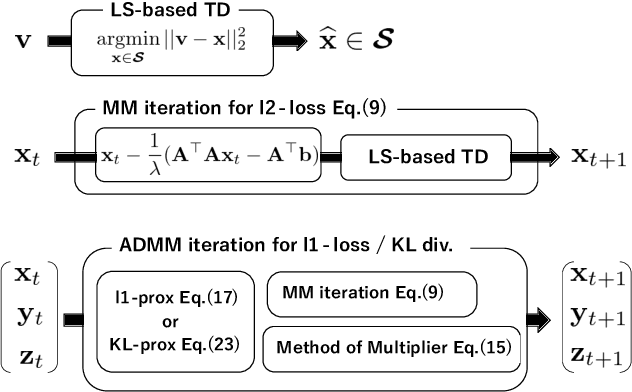
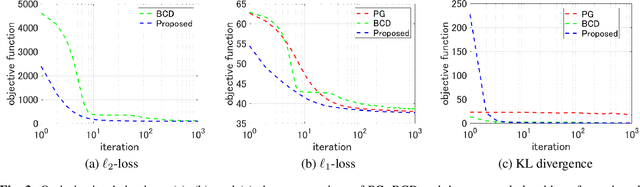
Abstract:In this paper, we propose a new unified optimization algorithm for general tensor decomposition which is formulated as an inverse problem for low-rank tensors in the general linear observation models. The proposed algorithm supports three basic loss functions ($\ell_2$-loss, $\ell_1$-loss and KL divergence) and various low-rank tensor decomposition models (CP, Tucker, TT, and TR decompositions). We derive the optimization algorithm based on hierarchical combination of the alternating direction method of multiplier (ADMM) and majorization-minimization (MM). We show that wide-range applications can be solved by the proposed algorithm, and can be easily extended to any established tensor decomposition models in a {plug-and-play} manner.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge