Soft Smoothness for Audio Inpainting Using a Latent Matrix Model in Delay-embedded Space
Paper and Code
Mar 18, 2022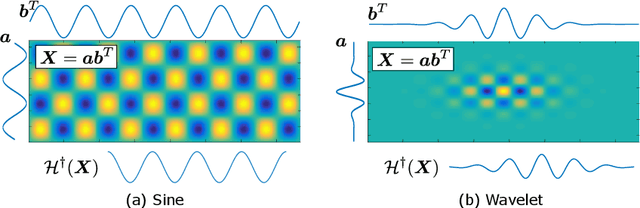

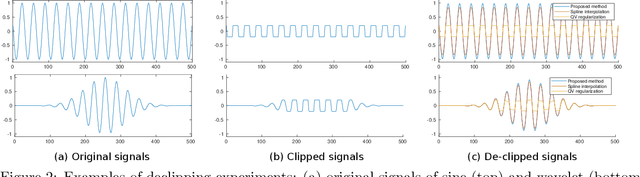
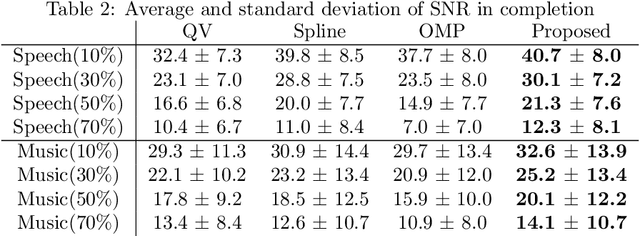
Here, we propose a new reconstruction method of smooth time-series signals. A key concept of this study is not considering the model in signal space, but in delay-embedded space. In other words, we indirectly represent a time-series signal as an output of inverse delay-embedding of a matrix, and the matrix is constrained. Based on the model under inverse delay-embedding, we propose to constrain the matrix to be rank-1 with smooth factor vectors. The proposed model is closely related to the convolutional model, and quadratic variation (QV) regularization. Especially, the proposed method can be characterized as a generalization of QV regularization. In addition, we show that the proposed method provides the softer smoothness than QV regularization. Experiments of audio inpainting and declipping are conducted to show its advantages in comparison with several existing interpolation methods and sparse modeling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge