Network EM Algorithm for Gaussian Mixture Model in Decentralized Federated Learning

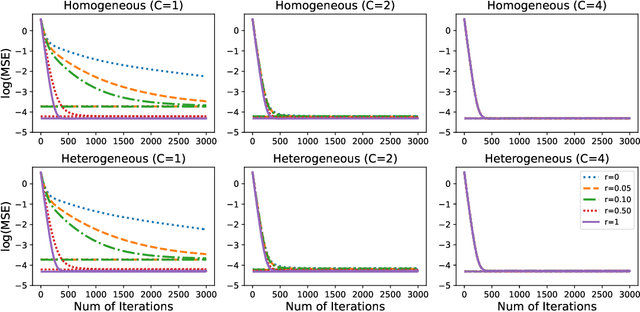
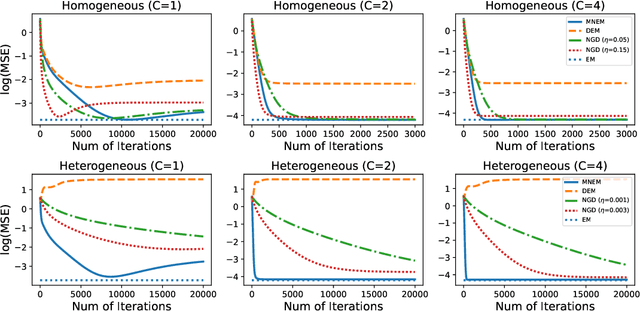
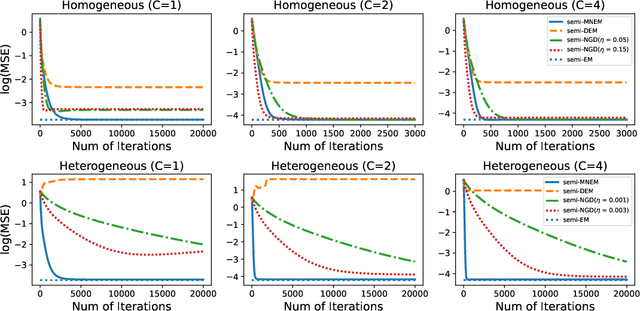
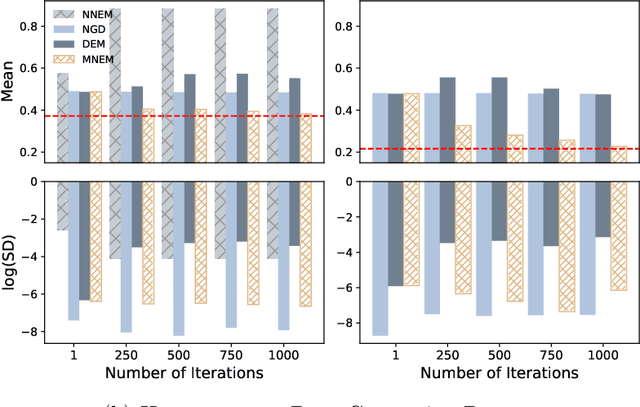
We systematically study various network Expectation-Maximization (EM) algorithms for the Gaussian mixture model within the framework of decentralized federated learning. Our theoretical investigation reveals that directly extending the classical decentralized supervised learning method to the EM algorithm exhibits poor estimation accuracy with heterogeneous data across clients and struggles to converge numerically when Gaussian components are poorly-separated. To address these issues, we propose two novel solutions. First, to handle heterogeneous data, we introduce a momentum network EM (MNEM) algorithm, which uses a momentum parameter to combine information from both the current and historical estimators. Second, to tackle the challenge of poorly-separated Gaussian components, we develop a semi-supervised MNEM (semi-MNEM) algorithm, which leverages partially labeled data. Rigorous theoretical analysis demonstrates that MNEM can achieve statistical efficiency comparable to that of the whole sample estimator when the mixture components satisfy certain separation conditions, even in heterogeneous scenarios. Moreover, the semi-MNEM estimator enhances the convergence speed of the MNEM algorithm, effectively addressing the numerical convergence challenges in poorly-separated scenarios. Extensive simulation and real data analyses are conducted to justify our theoretical findings.

A Selective Review on Statistical Methods for Massive Data Computation: Distributed Computing, Subsampling, and Minibatch Techniques

This paper presents a selective review of statistical computation methods for massive data analysis. A huge amount of statistical methods for massive data computation have been rapidly developed in the past decades. In this work, we focus on three categories of statistical computation methods: (1) distributed computing, (2) subsampling methods, and (3) minibatch gradient techniques. The first class of literature is about distributed computing and focuses on the situation, where the dataset size is too huge to be comfortably handled by one single computer. In this case, a distributed computation system with multiple computers has to be utilized. The second class of literature is about subsampling methods and concerns about the situation, where the sample size of dataset is small enough to be placed on one single computer but too large to be easily processed by its memory as a whole. The last class of literature studies those minibatch gradient related optimization techniques, which have been extensively used for optimizing various deep learning models.

Quasi-Newton Updating for Large-Scale Distributed Learning

Distributed computing is critically important for modern statistical analysis. Herein, we develop a distributed quasi-Newton (DQN) framework with excellent statistical, computation, and communication efficiency. In the DQN method, no Hessian matrix inversion or communication is needed. This considerably reduces the computation and communication complexity of the proposed method. Notably, related existing methods only analyze numerical convergence and require a diverging number of iterations to converge. However, we investigate the statistical properties of the DQN method and theoretically demonstrate that the resulting estimator is statistically efficient over a small number of iterations under mild conditions. Extensive numerical analyses demonstrate the finite sample performance.

Improved Naive Bayes with Mislabeled Data

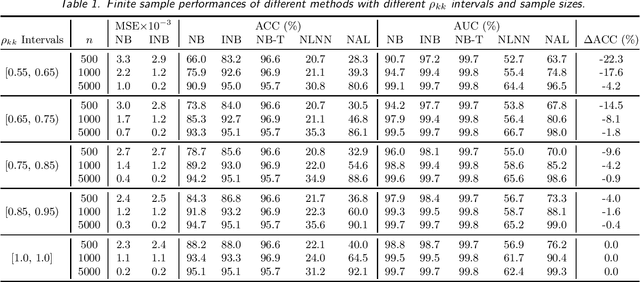
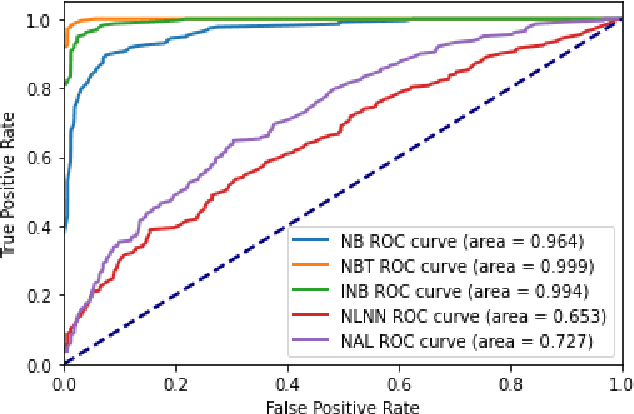
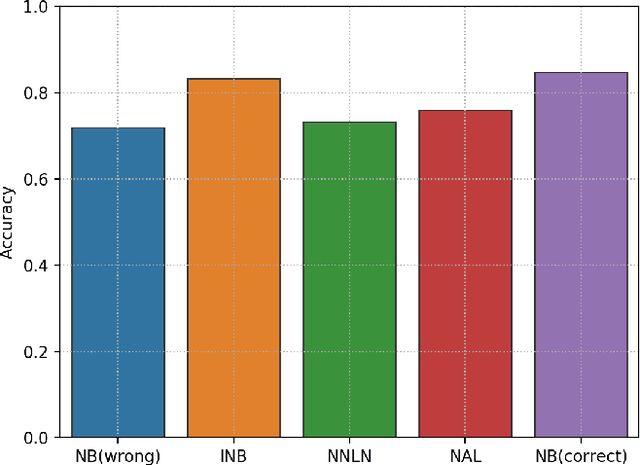
Labeling mistakes are frequently encountered in real-world applications. If not treated well, the labeling mistakes can deteriorate the classification performances of a model seriously. To address this issue, we propose an improved Naive Bayes method for text classification. It is analytically simple and free of subjective judgements on the correct and incorrect labels. By specifying the generating mechanism of incorrect labels, we optimize the corresponding log-likelihood function iteratively by using an EM algorithm. Our simulation and experiment results show that the improved Naive Bayes method greatly improves the performances of the Naive Bayes method with mislabeled data.

Embedding Compression for Text Classification Using Dictionary Screening

In this paper, we propose a dictionary screening method for embedding compression in text classification tasks. The key purpose of this method is to evaluate the importance of each keyword in the dictionary. To this end, we first train a pre-specified recurrent neural network-based model using a full dictionary. This leads to a benchmark model, which we then use to obtain the predicted class probabilities for each sample in a dataset. Next, to evaluate the impact of each keyword in affecting the predicted class probabilities, we develop a novel method for assessing the importance of each keyword in a dictionary. Consequently, each keyword can be screened, and only the most important keywords are reserved. With these screened keywords, a new dictionary with a considerably reduced size can be constructed. Accordingly, the original text sequence can be substantially compressed. The proposed method leads to significant reductions in terms of parameters, average text sequence, and dictionary size. Meanwhile, the prediction power remains very competitive compared to the benchmark model. Extensive numerical studies are presented to demonstrate the empirical performance of the proposed method.

Network Gradient Descent Algorithm for Decentralized Federated Learning

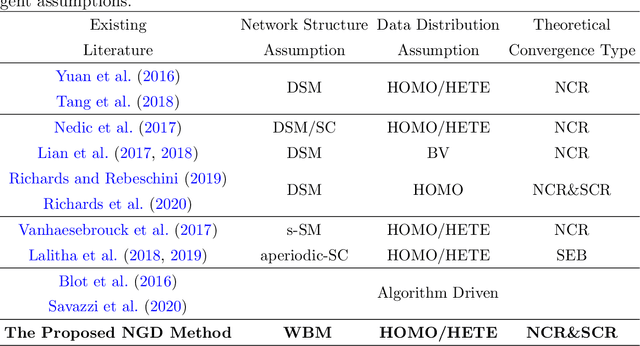
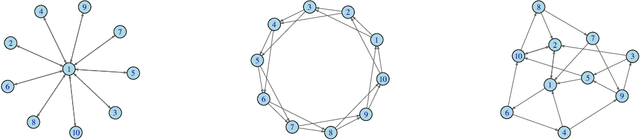
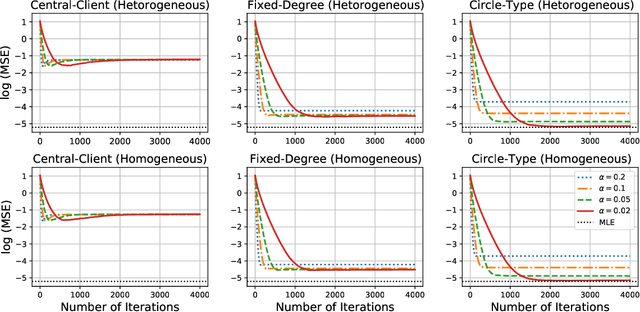
We study a fully decentralized federated learning algorithm, which is a novel gradient descent algorithm executed on a communication-based network. For convenience, we refer to it as a network gradient descent (NGD) method. In the NGD method, only statistics (e.g., parameter estimates) need to be communicated, minimizing the risk of privacy. Meanwhile, different clients communicate with each other directly according to a carefully designed network structure without a central master. This greatly enhances the reliability of the entire algorithm. Those nice properties inspire us to carefully study the NGD method both theoretically and numerically. Theoretically, we start with a classical linear regression model. We find that both the learning rate and the network structure play significant roles in determining the NGD estimator's statistical efficiency. The resulting NGD estimator can be statistically as efficient as the global estimator, if the learning rate is sufficiently small and the network structure is well balanced, even if the data are distributed heterogeneously. Those interesting findings are then extended to general models and loss functions. Extensive numerical studies are presented to corroborate our theoretical findings. Classical deep learning models are also presented for illustration purpose.

On the Subbagging Estimation for Massive Data

This article introduces subbagging (subsample aggregating) estimation approaches for big data analysis with memory constraints of computers. Specifically, for the whole dataset with size $N$, $m_N$ subsamples are randomly drawn, and each subsample with a subsample size $k_N\ll N$ to meet the memory constraint is sampled uniformly without replacement. Aggregating the estimators of $m_N$ subsamples can lead to subbagging estimation. To analyze the theoretical properties of the subbagging estimator, we adapt the incomplete $U$-statistics theory with an infinite order kernel to allow overlapping drawn subsamples in the sampling procedure. Utilizing this novel theoretical framework, we demonstrate that via a proper hyperparameter selection of $k_N$ and $m_N$, the subbagging estimator can achieve $\sqrt{N}$-consistency and asymptotic normality under the condition $(k_Nm_N)/N\to \alpha \in (0,\infty]$. Compared to the full sample estimator, we theoretically show that the $\sqrt{N}$-consistent subbagging estimator has an inflation rate of $1/\alpha$ in its asymptotic variance. Simulation experiments are presented to demonstrate the finite sample performances. An American airline dataset is analyzed to illustrate that the subbagging estimate is numerically close to the full sample estimate, and can be computationally fast under the memory constraint.

Hyperparameter Selection for Subsampling Bootstraps

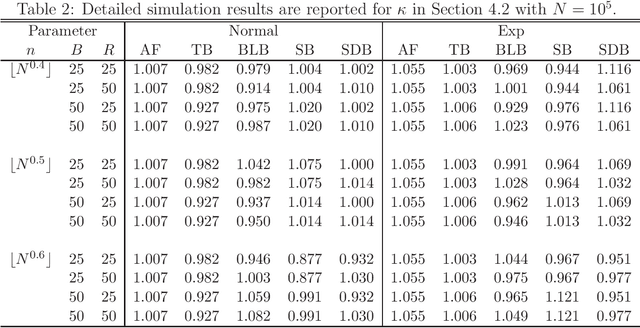
Massive data analysis becomes increasingly prevalent, subsampling methods like BLB (Bag of Little Bootstraps) serves as powerful tools for assessing the quality of estimators for massive data. However, the performance of the subsampling methods are highly influenced by the selection of tuning parameters ( e.g., the subset size, number of resamples per subset ). In this article we develop a hyperparameter selection methodology, which can be used to select tuning parameters for subsampling methods. Specifically, by a careful theoretical analysis, we find an analytically simple and elegant relationship between the asymptotic efficiency of various subsampling estimators and their hyperparameters. This leads to an optimal choice of the hyperparameters. More specifically, for an arbitrarily specified hyperparameter set, we can improve it to be a new set of hyperparameters with no extra CPU time cost, but the resulting estimator's statistical efficiency can be much improved. Both simulation studies and real data analysis demonstrate the superior advantage of our method.

Automatic, Dynamic, and Nearly Optimal Learning Rate Specification by Local Quadratic Approximation

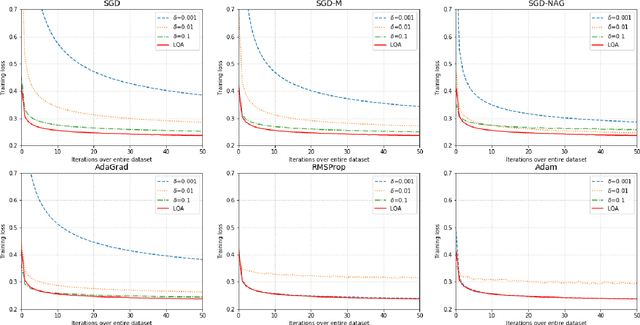
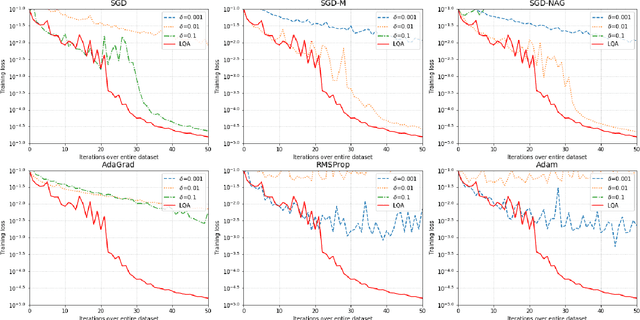
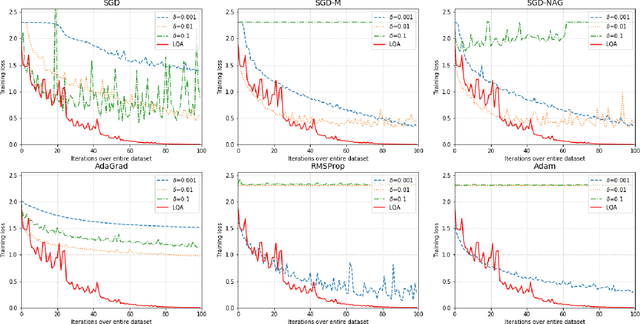
In deep learning tasks, the learning rate determines the update step size in each iteration, which plays a critical role in gradient-based optimization. However, the determination of the appropriate learning rate in practice typically replies on subjective judgement. In this work, we propose a novel optimization method based on local quadratic approximation (LQA). In each update step, given the gradient direction, we locally approximate the loss function by a standard quadratic function of the learning rate. Then, we propose an approximation step to obtain a nearly optimal learning rate in a computationally efficient way. The proposed LQA method has three important features. First, the learning rate is automatically determined in each update step. Second, it is dynamically adjusted according to the current loss function value and the parameter estimates. Third, with the gradient direction fixed, the proposed method leads to nearly the greatest reduction in terms of the loss function. Extensive experiments have been conducted to prove the strengths of the proposed LQA method.

Least Squares Approximation for a Distributed System

In this work we develop a distributed least squares approximation (DLSA) method, which is able to solve a large family of regression problems (e.g., linear regression, logistic regression, Cox's model) on a distributed system. By approximating the local objective function using a local quadratic form, we are able to obtain a combined estimator by taking a weighted average of local estimators. The resulting estimator is proved to be statistically as efficient as the global estimator. In the meanwhile it requires only one round of communication. We further conduct the shrinkage estimation based on the DLSA estimation by using an adaptive Lasso approach. The solution can be easily obtained by using the LARS algorithm on the master node. It is theoretically shown that the resulting estimator enjoys the oracle property and is selection consistent by using a newly designed distributed Bayesian Information Criterion (DBIC). The finite sample performance as well as the computational efficiency are further illustrated by extensive numerical study and an airline dataset. The airline dataset is 52GB in memory size. The entire methodology has been implemented by Python for a de-facto standard Spark system. By using the proposed DLSA algorithm on the Spark system, it takes 26 minutes to obtain a logistic regression estimator whereas a full likelihood algorithm takes 15 hours to reaches an inferior result.