DCA-LUT: Deep Chromatic Alignment with 5D LUT for Purple Fringing Removal

Purple fringing, a persistent artifact caused by Longitudinal Chromatic Aberration (LCA) in camera lenses, has long degraded the clarity and realism of digital imaging. Traditional solutions rely on complex and expensive apochromatic (APO) lens hardware and the extraction of handcrafted features, ignoring the data-driven approach. To fill this gap, we introduce DCA-LUT, the first deep learning framework for purple fringing removal. Inspired by the physical root of the problem, the spatial misalignment of RGB color channels due to lens dispersion, we introduce a novel Chromatic-Aware Coordinate Transformation (CA-CT) module, learning an image-adaptive color space to decouple and isolate fringing into a dedicated dimension. This targeted separation allows the network to learn a precise ``purple fringe channel", which then guides the accurate restoration of the luminance channel. The final color correction is performed by a learned 5D Look-Up Table (5D LUT), enabling efficient and powerful% non-linear color mapping. To enable robust training and fair evaluation, we constructed a large-scale synthetic purple fringing dataset (PF-Synth). Extensive experiments in synthetic and real-world datasets demonstrate that our method achieves state-of-the-art performance in purple fringing removal.

CAST-LUT: Tokenizer-Guided HSV Look-Up Tables for Purple Flare Removal

Purple flare, a diffuse chromatic aberration artifact commonly found around highlight areas, severely degrades the tone transition and color of the image. Existing traditional methods are based on hand-crafted features, which lack flexibility and rely entirely on fixed priors, while the scarcity of paired training data critically hampers deep learning. To address this issue, we propose a novel network built upon decoupled HSV Look-Up Tables (LUTs). The method aims to simplify color correction by adjusting the Hue (H), Saturation (S), and Value (V) components independently. This approach resolves the inherent color coupling problems in traditional methods. Our model adopts a two-stage architecture: First, a Chroma-Aware Spectral Tokenizer (CAST) converts the input image from RGB space to HSV space and independently encodes the Hue (H) and Value (V) channels into a set of semantic tokens describing the Purple flare status; second, the HSV-LUT module takes these tokens as input and dynamically generates independent correction curves (1D-LUTs) for the three channels H, S, and V. To effectively train and validate our model, we built the first large-scale purple flare dataset with diverse scenes. We also proposed new metrics and a loss function specifically designed for this task. Extensive experiments demonstrate that our model not only significantly outperforms existing methods in visual effects but also achieves state-of-the-art performance on all quantitative metrics.

UniFlowRestore: A General Video Restoration Framework via Flow Matching and Prompt Guidance

Video imaging is often affected by complex degradations such as blur, noise, and compression artifacts. Traditional restoration methods follow a "single-task single-model" paradigm, resulting in poor generalization and high computational cost, limiting their applicability in real-world scenarios with diverse degradation types. We propose UniFlowRestore, a general video restoration framework that models restoration as a time-continuous evolution under a prompt-guided and physics-informed vector field. A physics-aware backbone PhysicsUNet encodes degradation priors as potential energy, while PromptGenerator produces task-relevant prompts as momentum. These components define a Hamiltonian system whose vector field integrates inertial dynamics, decaying physical gradients, and prompt-based guidance. The system is optimized via a fixed-step ODE solver to achieve efficient and unified restoration across tasks. Experiments show that UniFlowRestore delivers stateof-the-art performance with strong generalization and efficiency. Quantitative results demonstrate that UniFlowRestore achieves state-of-the-art performance, attaining the highest PSNR (33.89 dB) and SSIM (0.97) on the video denoising task, while maintaining top or second-best scores across all evaluated tasks.

Convex Quaternion Optimization for Signal Processing: Theory and Applications

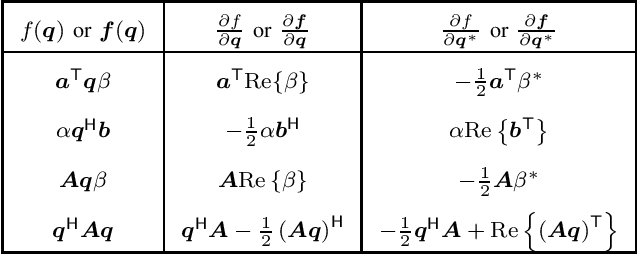
Convex optimization methods have been extensively used in the fields of communications and signal processing. However, the theory of quaternion optimization is currently not as fully developed and systematic as that of complex and real optimization. To this end, we establish an essential theory of convex quaternion optimization for signal processing based on the generalized Hamilton-real (GHR) calculus. This is achieved in a way which conforms with traditional complex and real optimization theory. For rigorous, We present five discriminant theorems for convex quaternion functions, and four discriminant criteria for strongly convex quaternion functions. Furthermore, we provide a fundamental theorem for the optimality of convex quaternion optimization problems, and demonstrate its utility through three applications in quaternion signal processing. These results provide a solid theoretical foundation for convex quaternion optimization and open avenues for further developments in signal processing applications.

Improved Naive Bayes with Mislabeled Data

Labeling mistakes are frequently encountered in real-world applications. If not treated well, the labeling mistakes can deteriorate the classification performances of a model seriously. To address this issue, we propose an improved Naive Bayes method for text classification. It is analytically simple and free of subjective judgements on the correct and incorrect labels. By specifying the generating mechanism of incorrect labels, we optimize the corresponding log-likelihood function iteratively by using an EM algorithm. Our simulation and experiment results show that the improved Naive Bayes method greatly improves the performances of the Naive Bayes method with mislabeled data.