A Selective Review on Statistical Methods for Massive Data Computation: Distributed Computing, Subsampling, and Minibatch Techniques

This paper presents a selective review of statistical computation methods for massive data analysis. A huge amount of statistical methods for massive data computation have been rapidly developed in the past decades. In this work, we focus on three categories of statistical computation methods: (1) distributed computing, (2) subsampling methods, and (3) minibatch gradient techniques. The first class of literature is about distributed computing and focuses on the situation, where the dataset size is too huge to be comfortably handled by one single computer. In this case, a distributed computation system with multiple computers has to be utilized. The second class of literature is about subsampling methods and concerns about the situation, where the sample size of dataset is small enough to be placed on one single computer but too large to be easily processed by its memory as a whole. The last class of literature studies those minibatch gradient related optimization techniques, which have been extensively used for optimizing various deep learning models.

Improved Naive Bayes with Mislabeled Data

Labeling mistakes are frequently encountered in real-world applications. If not treated well, the labeling mistakes can deteriorate the classification performances of a model seriously. To address this issue, we propose an improved Naive Bayes method for text classification. It is analytically simple and free of subjective judgements on the correct and incorrect labels. By specifying the generating mechanism of incorrect labels, we optimize the corresponding log-likelihood function iteratively by using an EM algorithm. Our simulation and experiment results show that the improved Naive Bayes method greatly improves the performances of the Naive Bayes method with mislabeled data.

Automatic, Dynamic, and Nearly Optimal Learning Rate Specification by Local Quadratic Approximation

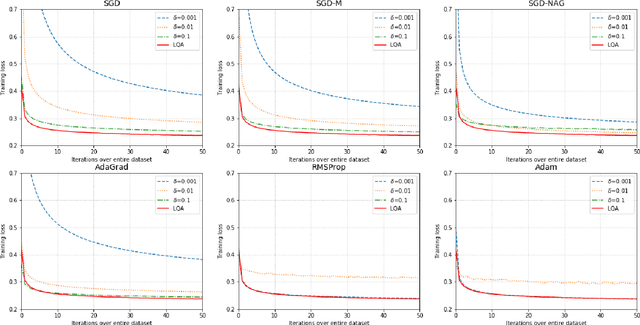
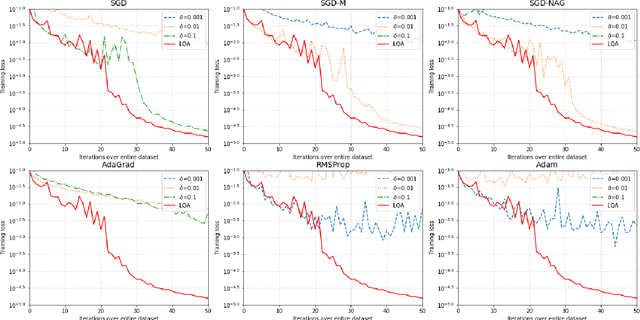
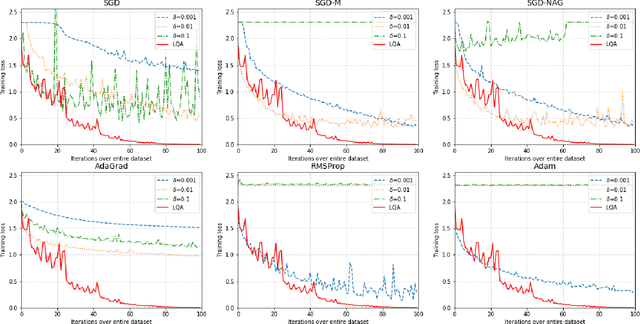
In deep learning tasks, the learning rate determines the update step size in each iteration, which plays a critical role in gradient-based optimization. However, the determination of the appropriate learning rate in practice typically replies on subjective judgement. In this work, we propose a novel optimization method based on local quadratic approximation (LQA). In each update step, given the gradient direction, we locally approximate the loss function by a standard quadratic function of the learning rate. Then, we propose an approximation step to obtain a nearly optimal learning rate in a computationally efficient way. The proposed LQA method has three important features. First, the learning rate is automatically determined in each update step. Second, it is dynamically adjusted according to the current loss function value and the parameter estimates. Third, with the gradient direction fixed, the proposed method leads to nearly the greatest reduction in terms of the loss function. Extensive experiments have been conducted to prove the strengths of the proposed LQA method.