A Selective Review on Statistical Methods for Massive Data Computation: Distributed Computing, Subsampling, and Minibatch Techniques

This paper presents a selective review of statistical computation methods for massive data analysis. A huge amount of statistical methods for massive data computation have been rapidly developed in the past decades. In this work, we focus on three categories of statistical computation methods: (1) distributed computing, (2) subsampling methods, and (3) minibatch gradient techniques. The first class of literature is about distributed computing and focuses on the situation, where the dataset size is too huge to be comfortably handled by one single computer. In this case, a distributed computation system with multiple computers has to be utilized. The second class of literature is about subsampling methods and concerns about the situation, where the sample size of dataset is small enough to be placed on one single computer but too large to be easily processed by its memory as a whole. The last class of literature studies those minibatch gradient related optimization techniques, which have been extensively used for optimizing various deep learning models.

Quasi-Newton Updating for Large-Scale Distributed Learning

Distributed computing is critically important for modern statistical analysis. Herein, we develop a distributed quasi-Newton (DQN) framework with excellent statistical, computation, and communication efficiency. In the DQN method, no Hessian matrix inversion or communication is needed. This considerably reduces the computation and communication complexity of the proposed method. Notably, related existing methods only analyze numerical convergence and require a diverging number of iterations to converge. However, we investigate the statistical properties of the DQN method and theoretically demonstrate that the resulting estimator is statistically efficient over a small number of iterations under mild conditions. Extensive numerical analyses demonstrate the finite sample performance.

Network Gradient Descent Algorithm for Decentralized Federated Learning

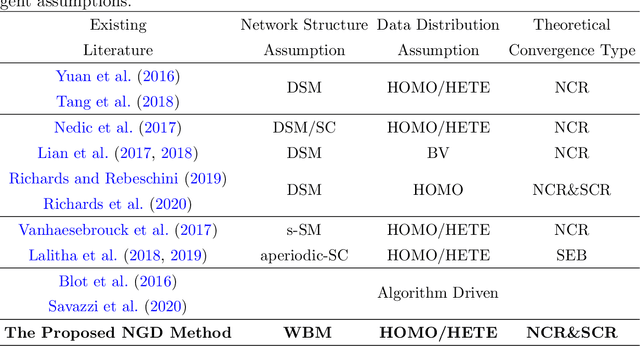
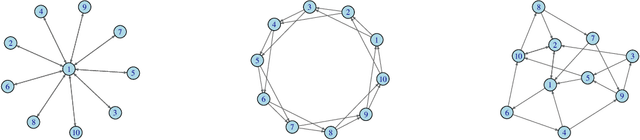
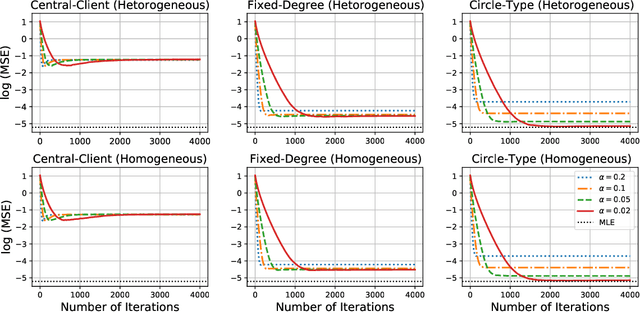
We study a fully decentralized federated learning algorithm, which is a novel gradient descent algorithm executed on a communication-based network. For convenience, we refer to it as a network gradient descent (NGD) method. In the NGD method, only statistics (e.g., parameter estimates) need to be communicated, minimizing the risk of privacy. Meanwhile, different clients communicate with each other directly according to a carefully designed network structure without a central master. This greatly enhances the reliability of the entire algorithm. Those nice properties inspire us to carefully study the NGD method both theoretically and numerically. Theoretically, we start with a classical linear regression model. We find that both the learning rate and the network structure play significant roles in determining the NGD estimator's statistical efficiency. The resulting NGD estimator can be statistically as efficient as the global estimator, if the learning rate is sufficiently small and the network structure is well balanced, even if the data are distributed heterogeneously. Those interesting findings are then extended to general models and loss functions. Extensive numerical studies are presented to corroborate our theoretical findings. Classical deep learning models are also presented for illustration purpose.

Vehicle Re-identification Method Based on Vehicle Attribute and Mutual Exclusion Between Cameras

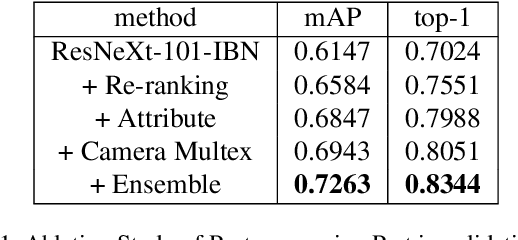
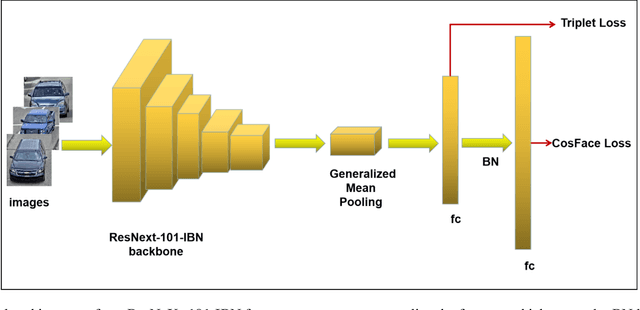
Vehicle Re-identification aims to identify a specific vehicle across time and camera view. With the rapid growth of intelligent transportation systems and smart cities, vehicle Re-identification technology gets more and more attention. However, due to the difference of shooting angle and the high similarity of vehicles belonging to the same brand, vehicle re-identification becomes a great challenge for existing method. In this paper, we propose a vehicle attribute-guided method to re-rank vehicle Re-ID result. The attributes used include vehicle orientation and vehicle brand . We also focus on the camera information and introduce camera mutual exclusion theory to further fine-tune the search results. In terms of feature extraction, we combine the data augmentations of multi-resolutions with the large model ensemble to get a more robust vehicle features. Our method achieves mAP of 63.73% and rank-1 accuracy 76.61% in the CVPR 2021 AI City Challenge.

Automatic, Dynamic, and Nearly Optimal Learning Rate Specification by Local Quadratic Approximation

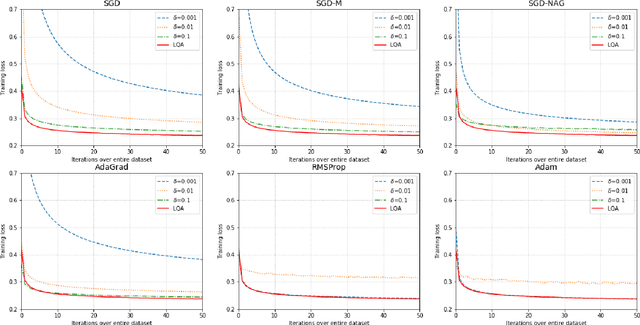
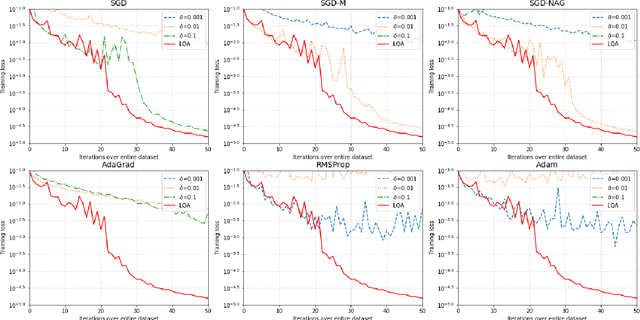
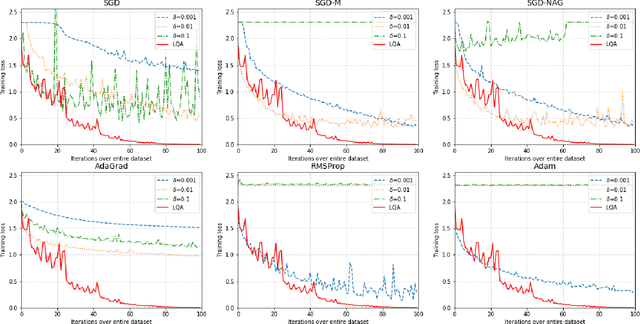
In deep learning tasks, the learning rate determines the update step size in each iteration, which plays a critical role in gradient-based optimization. However, the determination of the appropriate learning rate in practice typically replies on subjective judgement. In this work, we propose a novel optimization method based on local quadratic approximation (LQA). In each update step, given the gradient direction, we locally approximate the loss function by a standard quadratic function of the learning rate. Then, we propose an approximation step to obtain a nearly optimal learning rate in a computationally efficient way. The proposed LQA method has three important features. First, the learning rate is automatically determined in each update step. Second, it is dynamically adjusted according to the current loss function value and the parameter estimates. Third, with the gradient direction fixed, the proposed method leads to nearly the greatest reduction in terms of the loss function. Extensive experiments have been conducted to prove the strengths of the proposed LQA method.