A Selective Review on Statistical Methods for Massive Data Computation: Distributed Computing, Subsampling, and Minibatch Techniques

This paper presents a selective review of statistical computation methods for massive data analysis. A huge amount of statistical methods for massive data computation have been rapidly developed in the past decades. In this work, we focus on three categories of statistical computation methods: (1) distributed computing, (2) subsampling methods, and (3) minibatch gradient techniques. The first class of literature is about distributed computing and focuses on the situation, where the dataset size is too huge to be comfortably handled by one single computer. In this case, a distributed computation system with multiple computers has to be utilized. The second class of literature is about subsampling methods and concerns about the situation, where the sample size of dataset is small enough to be placed on one single computer but too large to be easily processed by its memory as a whole. The last class of literature studies those minibatch gradient related optimization techniques, which have been extensively used for optimizing various deep learning models.

Hyperparameter Selection for Subsampling Bootstraps

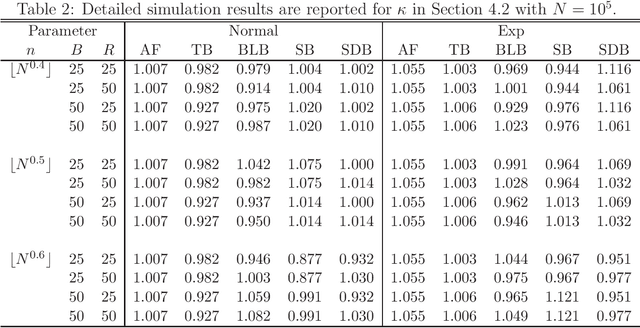
Massive data analysis becomes increasingly prevalent, subsampling methods like BLB (Bag of Little Bootstraps) serves as powerful tools for assessing the quality of estimators for massive data. However, the performance of the subsampling methods are highly influenced by the selection of tuning parameters ( e.g., the subset size, number of resamples per subset ). In this article we develop a hyperparameter selection methodology, which can be used to select tuning parameters for subsampling methods. Specifically, by a careful theoretical analysis, we find an analytically simple and elegant relationship between the asymptotic efficiency of various subsampling estimators and their hyperparameters. This leads to an optimal choice of the hyperparameters. More specifically, for an arbitrarily specified hyperparameter set, we can improve it to be a new set of hyperparameters with no extra CPU time cost, but the resulting estimator's statistical efficiency can be much improved. Both simulation studies and real data analysis demonstrate the superior advantage of our method.