Network Gradient Descent Algorithm for Decentralized Federated Learning
Paper and Code
May 06, 2022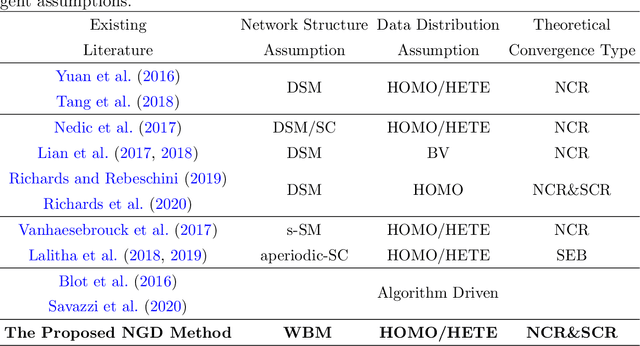
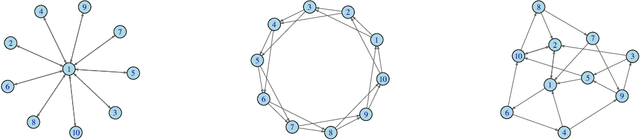

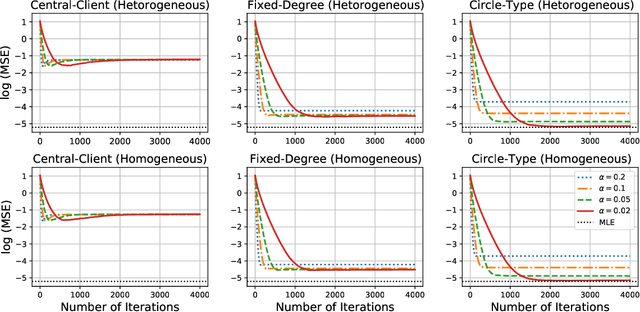
We study a fully decentralized federated learning algorithm, which is a novel gradient descent algorithm executed on a communication-based network. For convenience, we refer to it as a network gradient descent (NGD) method. In the NGD method, only statistics (e.g., parameter estimates) need to be communicated, minimizing the risk of privacy. Meanwhile, different clients communicate with each other directly according to a carefully designed network structure without a central master. This greatly enhances the reliability of the entire algorithm. Those nice properties inspire us to carefully study the NGD method both theoretically and numerically. Theoretically, we start with a classical linear regression model. We find that both the learning rate and the network structure play significant roles in determining the NGD estimator's statistical efficiency. The resulting NGD estimator can be statistically as efficient as the global estimator, if the learning rate is sufficiently small and the network structure is well balanced, even if the data are distributed heterogeneously. Those interesting findings are then extended to general models and loss functions. Extensive numerical studies are presented to corroborate our theoretical findings. Classical deep learning models are also presented for illustration purpose.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge