Yang Weng
ExARNN: An Environment-Driven Adaptive RNN for Learning Non-Stationary Power Dynamics
May 23, 2025Abstract:Non-stationary power system dynamics, influenced by renewable energy variability, evolving demand patterns, and climate change, are becoming increasingly complex. Accurately capturing these dynamics requires a model capable of adapting to environmental factors. Traditional models, including Recurrent Neural Networks (RNNs), lack efficient mechanisms to encode external factors, such as time or environmental data, for dynamic adaptation. To address this, we propose the External Adaptive RNN (ExARNN), a novel framework that integrates external data (e.g., weather, time) to continuously adjust the parameters of a base RNN. ExARNN achieves this through a hierarchical hypernetwork design, using Neural Controlled Differential Equations (NCDE) to process external data and generate RNN parameters adaptively. This approach enables ExARNN to handle inconsistent timestamps between power and external measurements, ensuring continuous adaptation. Extensive forecasting tests demonstrate ExARNN's superiority over established baseline models.
UniFlowRestore: A General Video Restoration Framework via Flow Matching and Prompt Guidance
Apr 12, 2025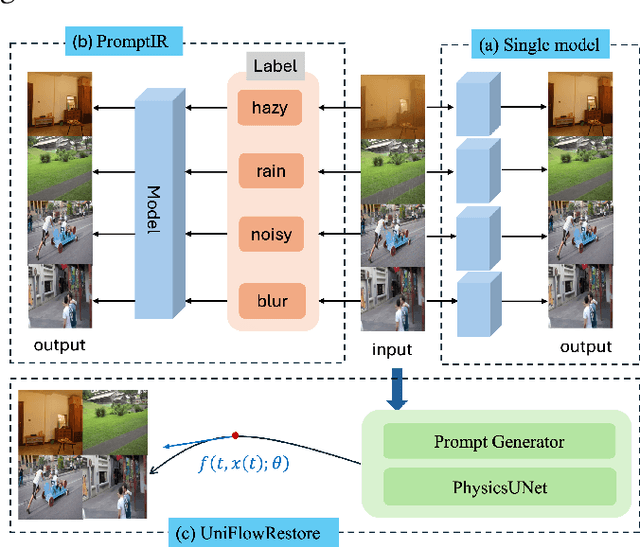

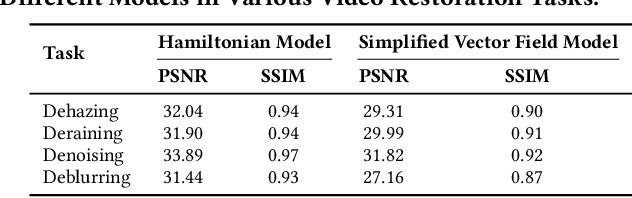

Abstract:Video imaging is often affected by complex degradations such as blur, noise, and compression artifacts. Traditional restoration methods follow a "single-task single-model" paradigm, resulting in poor generalization and high computational cost, limiting their applicability in real-world scenarios with diverse degradation types. We propose UniFlowRestore, a general video restoration framework that models restoration as a time-continuous evolution under a prompt-guided and physics-informed vector field. A physics-aware backbone PhysicsUNet encodes degradation priors as potential energy, while PromptGenerator produces task-relevant prompts as momentum. These components define a Hamiltonian system whose vector field integrates inertial dynamics, decaying physical gradients, and prompt-based guidance. The system is optimized via a fixed-step ODE solver to achieve efficient and unified restoration across tasks. Experiments show that UniFlowRestore delivers stateof-the-art performance with strong generalization and efficiency. Quantitative results demonstrate that UniFlowRestore achieves state-of-the-art performance, attaining the highest PSNR (33.89 dB) and SSIM (0.97) on the video denoising task, while maintaining top or second-best scores across all evaluated tasks.
Distribution Grid Line Outage Identification with Unknown Pattern and Performance Guarantee
Sep 10, 2023Abstract:Line outage identification in distribution grids is essential for sustainable grid operation. In this work, we propose a practical yet robust detection approach that utilizes only readily available voltage magnitudes, eliminating the need for costly phase angles or power flow data. Given the sensor data, many existing detection methods based on change-point detection require prior knowledge of outage patterns, which are unknown for real-world outage scenarios. To remove this impractical requirement, we propose a data-driven method to learn the parameters of the post-outage distribution through gradient descent. However, directly using gradient descent presents feasibility issues. To address this, we modify our approach by adding a Bregman divergence constraint to control the trajectory of the parameter updates, which eliminates the feasibility problems. As timely operation is the key nowadays, we prove that the optimal parameters can be learned with convergence guarantees via leveraging the statistical and physical properties of voltage data. We evaluate our approach using many representative distribution grids and real load profiles with 17 outage configurations. The results show that we can detect and localize the outage in a timely manner with only voltage magnitudes and without assuming a prior knowledge of outage patterns.
* 12 pages
Digital twins of nonlinear dynamical systems
Oct 05, 2022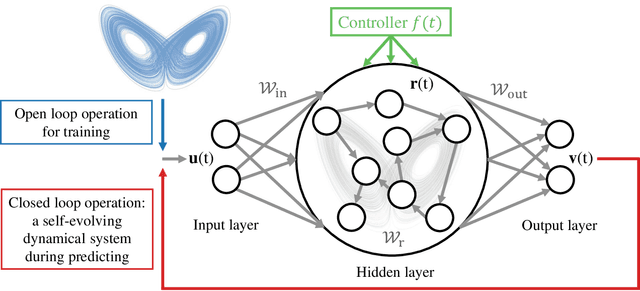
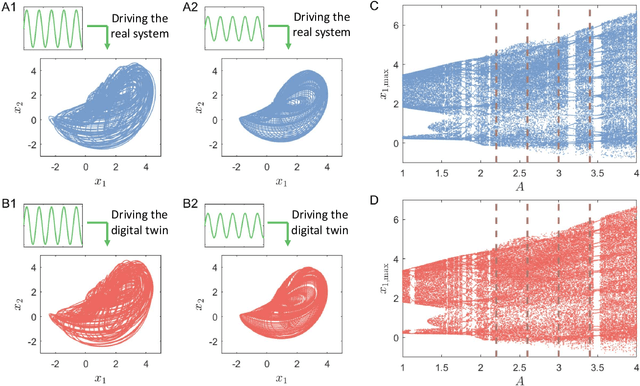
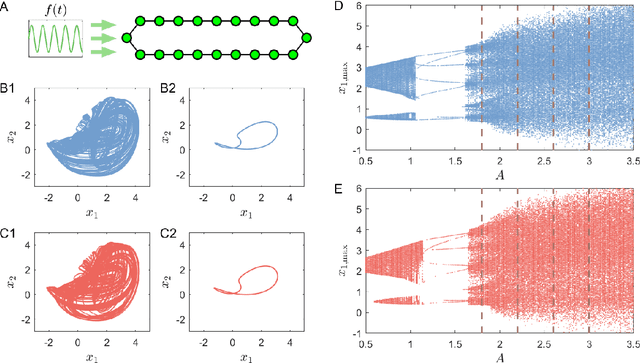
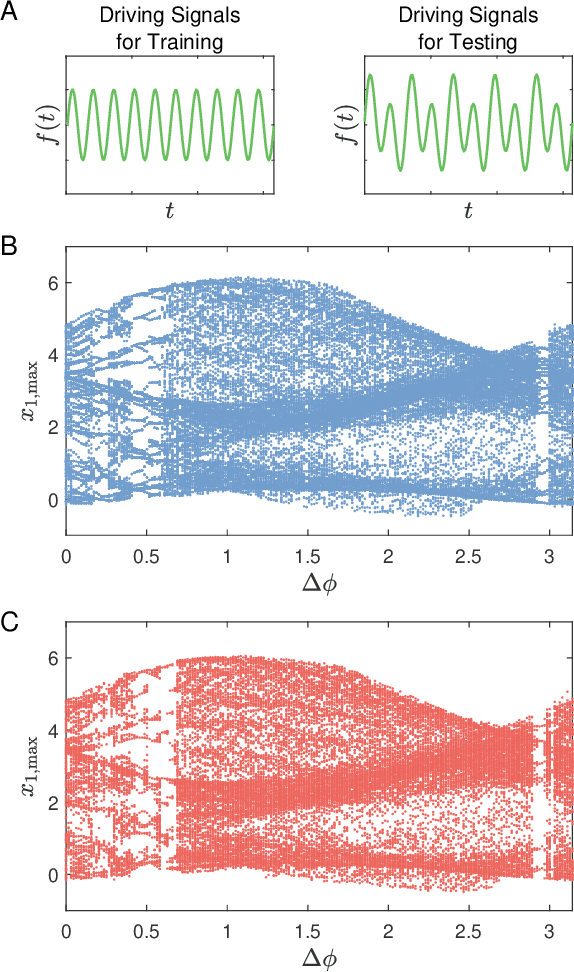
Abstract:We articulate the design imperatives for machine-learning based digital twins for nonlinear dynamical systems subject to external driving, which can be used to monitor the ``health'' of the target system and anticipate its future collapse. We demonstrate that, with single or parallel reservoir computing configurations, the digital twins are capable of challenging forecasting and monitoring tasks. Employing prototypical systems from climate, optics and ecology, we show that the digital twins can extrapolate the dynamics of the target system to certain parameter regimes never experienced before, make continual forecasting/monitoring with sparse real-time updates under non-stationary external driving, infer hidden variables and accurately predict their dynamical evolution, adapt to different forms of external driving, and extrapolate the global bifurcation behaviors to systems of some different sizes. These features make our digital twins appealing in significant applications such as monitoring the health of critical systems and forecasting their potential collapse induced by environmental changes.
CoNSoLe: Convex Neural Symbolic Learning
Jun 01, 2022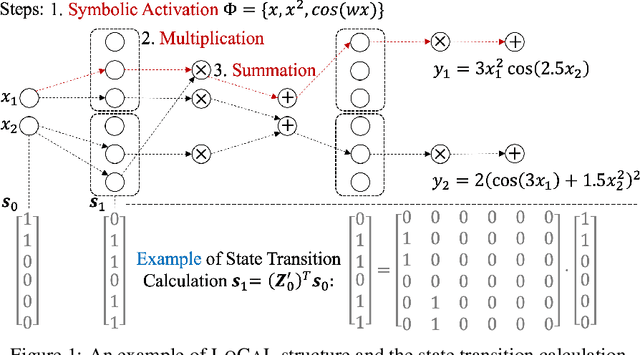

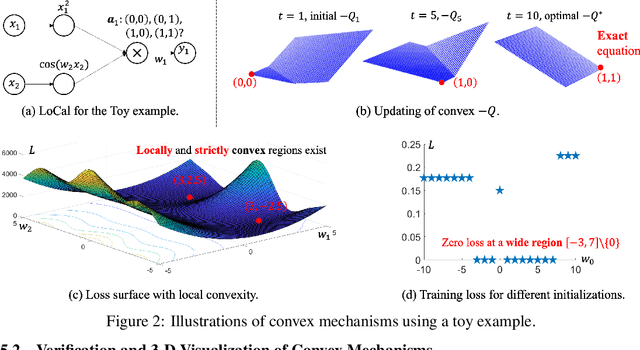
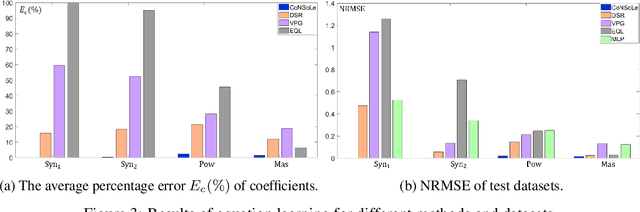
Abstract:Learning the underlying equation from data is a fundamental problem in many disciplines. Recent advances rely on Neural Networks (NNs) but do not provide theoretical guarantees in obtaining the exact equations owing to the non-convexity of NNs. In this paper, we propose Convex Neural Symbolic Learning (CoNSoLe) to seek convexity under mild conditions. The main idea is to decompose the recovering process into two steps and convexify each step. In the first step of searching for right symbols, we convexify the deep Q-learning. The key is to maintain double convexity for both the negative Q-function and the negative reward function in each iteration, leading to provable convexity of the negative optimal Q function to learn the true symbol connections. Conditioned on the exact searching result, we construct a Locally Convex equation Learner (LoCaL) neural network to convexify the estimation of symbol coefficients. With such a design, we quantify a large region with strict convexity in the loss surface of LoCaL for commonly used physical functions. Finally, we demonstrate the superior performance of the CoNSoLe framework over the state-of-the-art on a diverse set of datasets.
Explainable Graph Theory-Based Identification of Meter-Transformer Mapping
May 19, 2022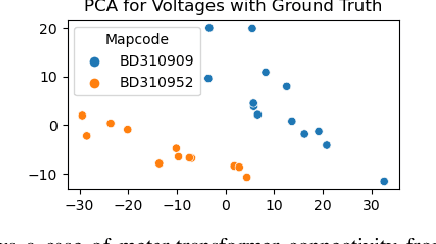

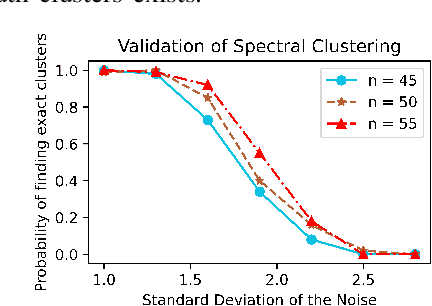
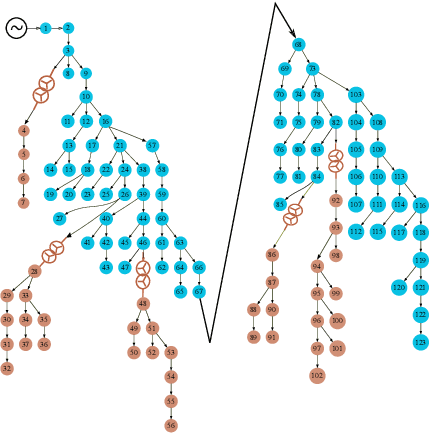
Abstract:Distributed energy resources are better for the environment but may cause transformer overload in distribution grids, calling for recovering meter-transformer mapping to provide situational awareness, i.e., the transformer loading. The challenge lies in recovering meter-transformer (M.T.) mapping for two common scenarios, e.g., large distances between a meter and its parent transformer or high similarity of a meter's consumption pattern to a non-parent transformer's meters. Past methods either assume a variety of data as in the transmission grid or ignore the two common scenarios mentioned above. Therefore, we propose to utilize the above observation via spectral embedding by using the property that inter-transformer meter consumptions are not the same and that the noise in data is limited so that all the k smallest eigenvalues of the voltage-based Laplacian matrix are smaller than the next smallest eigenvalue of the ideal Laplacian matrix. We also provide a guarantee based on this understanding. Furthermore, we partially relax the assumption by utilizing location information to aid voltage information for areas geographically far away but with similar voltages. Numerical simulations on the IEEE test systems and real feeders from our partner utility show that the proposed method correctly identifies M.T. mapping.
Curriculum Based Reinforcement Learning of Grid Topology Controllers to Prevent Thermal Cascading
Dec 18, 2021

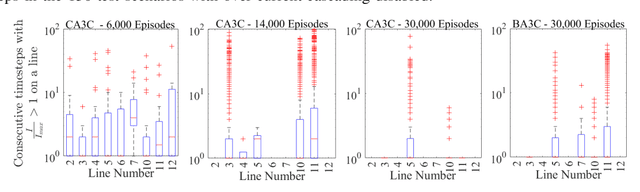

Abstract:This paper describes how domain knowledge of power system operators can be integrated into reinforcement learning (RL) frameworks to effectively learn agents that control the grid's topology to prevent thermal cascading. Typical RL-based topology controllers fail to perform well due to the large search/optimization space. Here, we propose an actor-critic-based agent to address the problem's combinatorial nature and train the agent using the RL environment developed by RTE, the French TSO. To address the challenge of the large optimization space, a curriculum-based approach with reward tuning is incorporated into the training procedure by modifying the environment using network physics for enhanced agent learning. Further, a parallel training approach on multiple scenarios is employed to avoid biasing the agent to a few scenarios and make it robust to the natural variability in grid operations. Without these modifications to the training procedure, the RL agent failed for most test scenarios, illustrating the importance of properly integrating domain knowledge of physical systems for real-world RL learning. The agent was tested by RTE for the 2019 learning to run the power network challenge and was awarded the 2nd place in accuracy and 1st place in speed. The developed code is open-sourced for public use.
The Powerful Use of AI in the Energy Sector: Intelligent Forecasting
Nov 03, 2021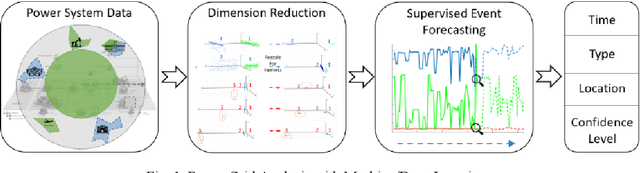
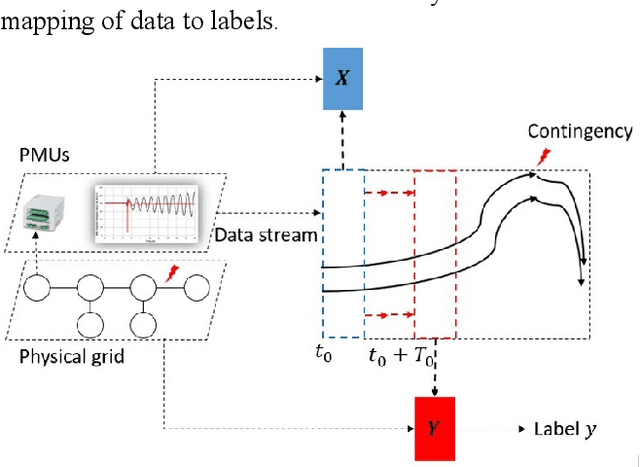
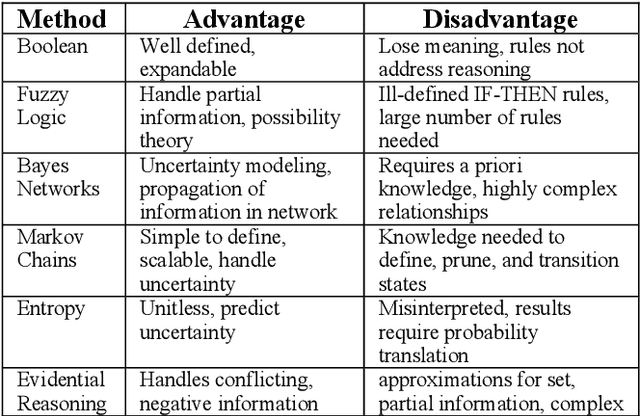
Abstract:Artificial Intelligence (AI) techniques continue to broaden across governmental and public sectors, such as power and energy - which serve as critical infrastructures for most societal operations. However, due to the requirements of reliability, accountability, and explainability, it is risky to directly apply AI-based methods to power systems because society cannot afford cascading failures and large-scale blackouts, which easily cost billions of dollars. To meet society requirements, this paper proposes a methodology to develop, deploy, and evaluate AI systems in the energy sector by: (1) understanding the power system measurements with physics, (2) designing AI algorithms to forecast the need, (3) developing robust and accountable AI methods, and (4) creating reliable measures to evaluate the performance of the AI model. The goal is to provide a high level of confidence to energy utility users. For illustration purposes, the paper uses power system event forecasting (PEF) as an example, which carefully analyzes synchrophasor patterns measured by the Phasor Measurement Units (PMUs). Such a physical understanding leads to a data-driven framework that reduces the dimensionality with physics and forecasts the event with high credibility. Specifically, for dimensionality reduction, machine learning arranges physical information from different dimensions, resulting inefficient information extraction. For event forecasting, the supervised learning model fuses the results of different models to increase the confidence. Finally, comprehensive experiments demonstrate the high accuracy, efficiency, and reliability as compared to other state-of-the-art machine learning methods.
Quick Line Outage Identification in Urban Distribution Grids via Smart Meters
Apr 01, 2021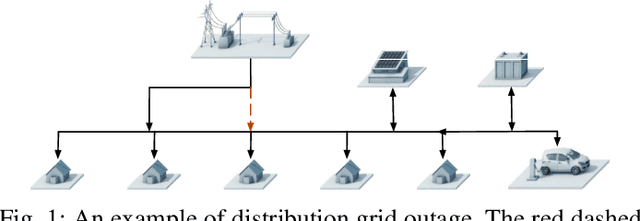

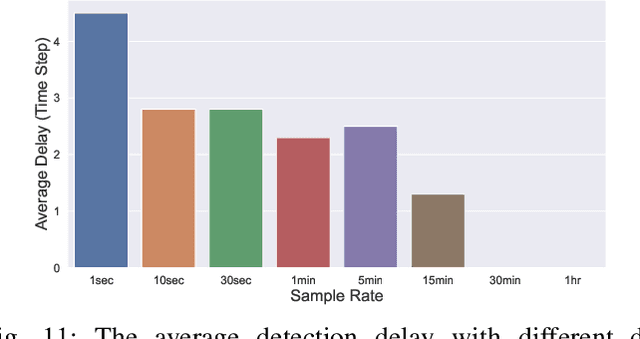
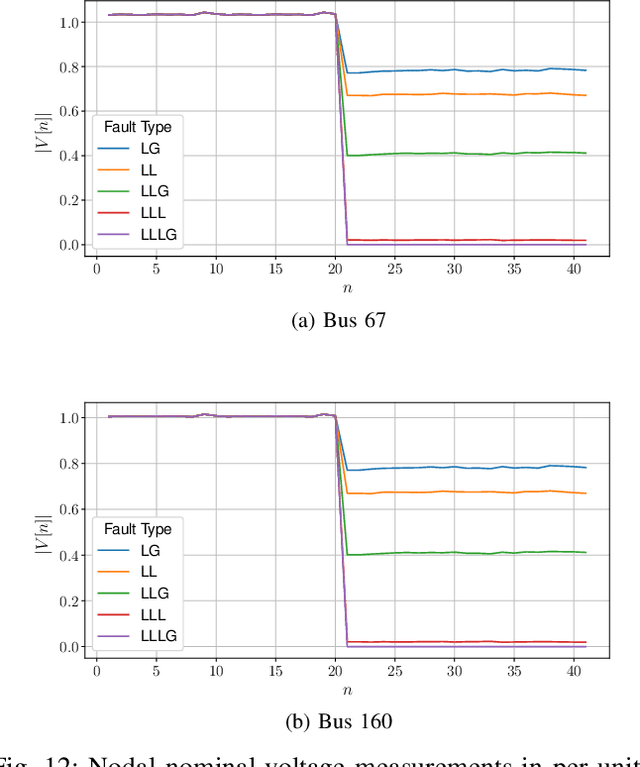
Abstract:The growing integration of distributed energy resources (DERs) in distribution grids raises various reliability issues due to DER's uncertain and complex behaviors. With a large-scale DER penetration in distribution grids, traditional outage detection methods, which rely on customers report and smart meters' last gasp signals, will have poor performance, because the renewable generators and storages and the mesh structure in urban distribution grids can continue supplying power after line outages. To address these challenges, we propose a data-driven outage monitoring approach based on the stochastic time series analysis with a theoretical guarantee. Specifically, we prove via power flow analysis that the dependency of time-series voltage measurements exhibits significant statistical changes after line outages. This makes the theory on optimal change-point detection suitable to identify line outages. However, existing change point detection methods require post-outage voltage distribution, which is unknown in distribution systems. Therefore, we design a maximum likelihood estimator to directly learn the distribution parameters from voltage data. We prove that the estimated parameters-based detection also achieves the optimal performance, making it extremely useful for fast distribution grid outage identifications. Furthermore, since smart meters have been widely installed in distribution grids and advanced infrastructure (e.g., PMU) has not widely been available, our approach only requires voltage magnitude for quick outage identification. Simulation results show highly accurate outage identification in eight distribution grids with 14 configurations with and without DERs using smart meter data.
Fast Distribution Grid Line Outage Identification with $μ$PMU
Nov 14, 2018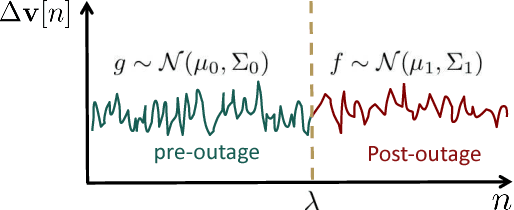
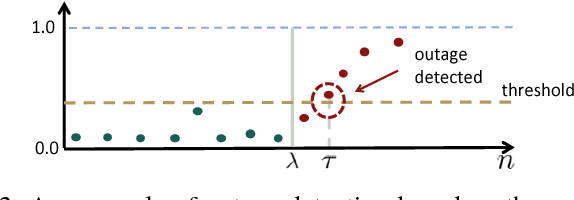
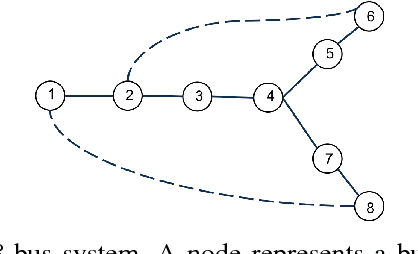
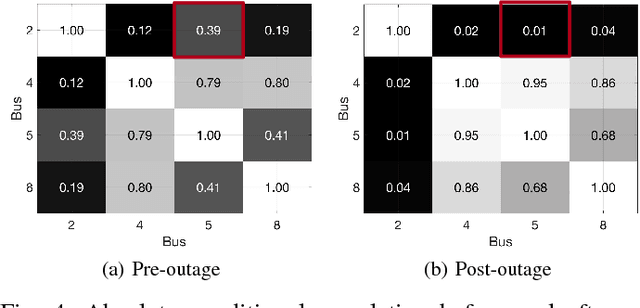
Abstract:The growing integration of distributed energy resources (DERs) in urban distribution grids raises various reliability issues due to DER's uncertain and complex behaviors. With a large-scale DER penetration, traditional outage detection methods, which rely on customers making phone calls and smart meters' "last gasp" signals, will have limited performance, because the renewable generators can supply powers after line outages and many urban grids are mesh so line outages do not affect power supply. To address these drawbacks, we propose a data-driven outage monitoring approach based on the stochastic time series analysis from micro phasor measurement unit ($\mu$PMU). Specifically, we prove via power flow analysis that the dependency of time-series voltage measurements exhibits significant statistical changes after line outages. This makes the theory on optimal change-point detection suitable to identify line outages via $\mu$PMUs with fast and accurate sampling. However, existing change point detection methods require post-outage voltage distribution unknown in distribution systems. Therefore, we design a maximum likelihood-based method to directly learn the distribution parameters from $\mu$PMU data. We prove that the estimated parameters-based detection still achieves the optimal performance, making it extremely useful for distribution grid outage identifications. Simulation results show highly accurate outage identification in eight distribution grids with 14 configurations with and without DERs using $\mu$PMU data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge