Machine-learning prediction of tipping and collapse of the Atlantic Meridional Overturning Circulation

Recent research on the Atlantic Meridional Overturning Circulation (AMOC) raised concern about its potential collapse through a tipping point due to the climate-change caused increase in the freshwater input into the North Atlantic. The predicted time window of collapse is centered about the middle of the century and the earliest possible start is approximately two years from now. More generally, anticipating a tipping point at which the system transitions from one stable steady state to another is relevant to a broad range of fields. We develop a machine-learning approach to predicting tipping in noisy dynamical systems with a time-varying parameter and test it on a number of systems including the AMOC, ecological networks, an electrical power system, and a climate model. For the AMOC, our prediction based on simulated fingerprint data and real data of the sea surface temperature places the time window of a potential collapse between the years 2040 and 2065.

Machine-learning parameter tracking with partial state observation

Complex and nonlinear dynamical systems often involve parameters that change with time, accurate tracking of which is essential to tasks such as state estimation, prediction, and control. Existing machine-learning methods require full state observation of the underlying system and tacitly assume adiabatic changes in the parameter. Formulating an inverse problem and exploiting reservoir computing, we develop a model-free and fully data-driven framework to accurately track time-varying parameters from partial state observation in real time. In particular, with training data from a subset of the dynamical variables of the system for a small number of known parameter values, the framework is able to accurately predict the parameter variations in time. Low- and high-dimensional, Markovian and non-Markovian nonlinear dynamical systems are used to demonstrate the power of the machine-learning based parameter-tracking framework. Pertinent issues affecting the tracking performance are addressed.

Model-free tracking control of complex dynamical trajectories with machine learning

Nonlinear tracking control enabling a dynamical system to track a desired trajectory is fundamental to robotics, serving a wide range of civil and defense applications. In control engineering, designing tracking control requires complete knowledge of the system model and equations. We develop a model-free, machine-learning framework to control a two-arm robotic manipulator using only partially observed states, where the controller is realized by reservoir computing. Stochastic input is exploited for training, which consists of the observed partial state vector as the first and its immediate future as the second component so that the neural machine regards the latter as the future state of the former. In the testing (deployment) phase, the immediate-future component is replaced by the desired observational vector from the reference trajectory. We demonstrate the effectiveness of the control framework using a variety of periodic and chaotic signals, and establish its robustness against measurement noise, disturbances, and uncertainties.

Digital twins of nonlinear dynamical systems

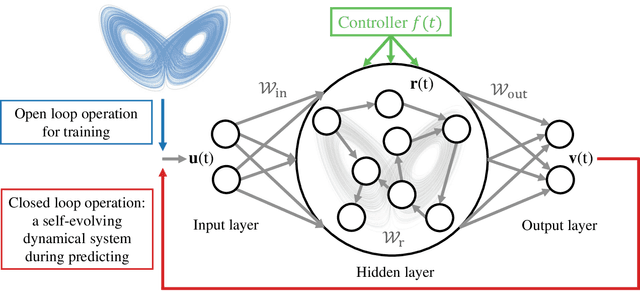
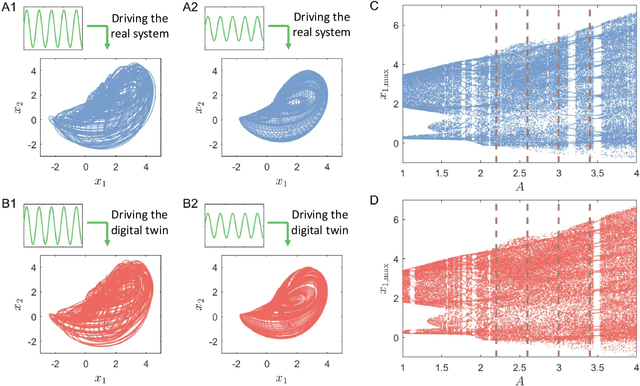
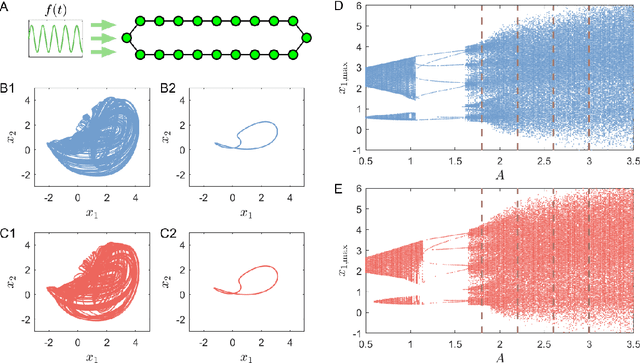
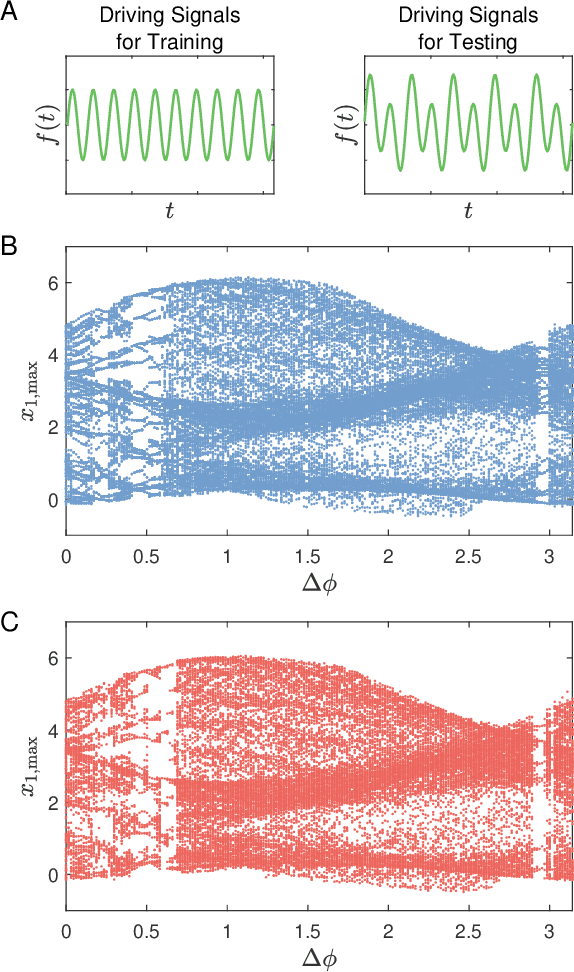
We articulate the design imperatives for machine-learning based digital twins for nonlinear dynamical systems subject to external driving, which can be used to monitor the ``health'' of the target system and anticipate its future collapse. We demonstrate that, with single or parallel reservoir computing configurations, the digital twins are capable of challenging forecasting and monitoring tasks. Employing prototypical systems from climate, optics and ecology, we show that the digital twins can extrapolate the dynamics of the target system to certain parameter regimes never experienced before, make continual forecasting/monitoring with sparse real-time updates under non-stationary external driving, infer hidden variables and accurately predict their dynamical evolution, adapt to different forms of external driving, and extrapolate the global bifurcation behaviors to systems of some different sizes. These features make our digital twins appealing in significant applications such as monitoring the health of critical systems and forecasting their potential collapse induced by environmental changes.

Tomography of time-dependent quantum spin networks with machine learning

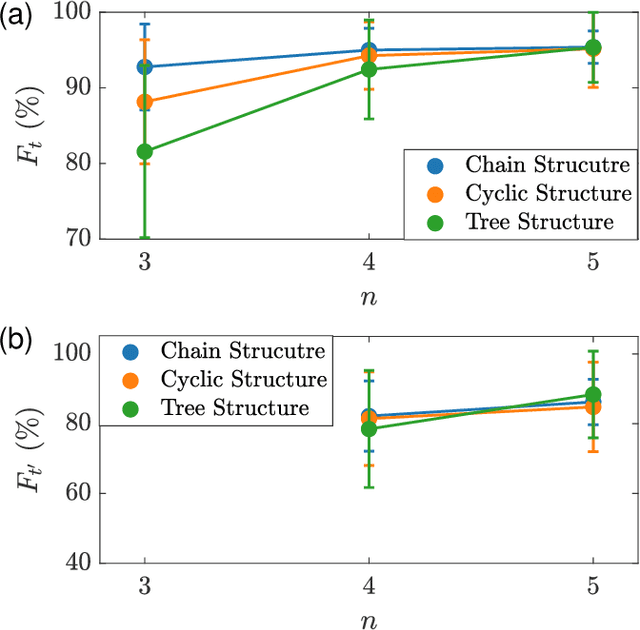
Interacting spin networks are fundamental to quantum computing. Data-based tomography of time-independent spin networks has been achieved, but an open challenge is to ascertain the structures of time-dependent spin networks using time series measurements taken locally from a small subset of the spins. Physically, the dynamical evolution of a spin network under time-dependent driving or perturbation is described by the Heisenberg equation of motion. Motivated by this basic fact, we articulate a physics-enhanced machine learning framework whose core is Heisenberg neural networks. In particular, we develop a deep learning algorithm according to some physics motivated loss function based on the Heisenberg equation, which "forces" the neural network to follow the quantum evolution of the spin variables. We demonstrate that, from local measurements, not only the local Hamiltonian can be recovered but the Hamiltonian reflecting the interacting structure of the whole system can also be faithfully reconstructed. We test our Heisenberg neural machine on spin networks of a variety of structures. In the extreme case where measurements are taken from only one spin, the achieved tomography fidelity values can reach about 90%. The developed machine learning framework is applicable to any time-dependent systems whose quantum dynamical evolution is governed by the Heisenberg equation of motion.

Adaptable Hamiltonian neural networks

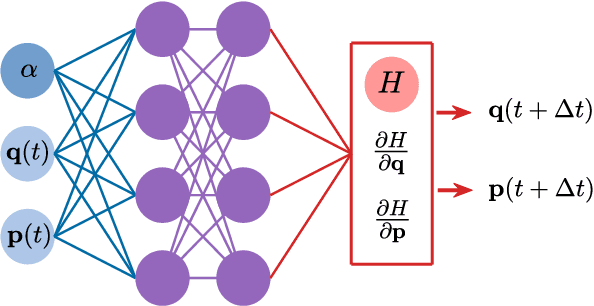
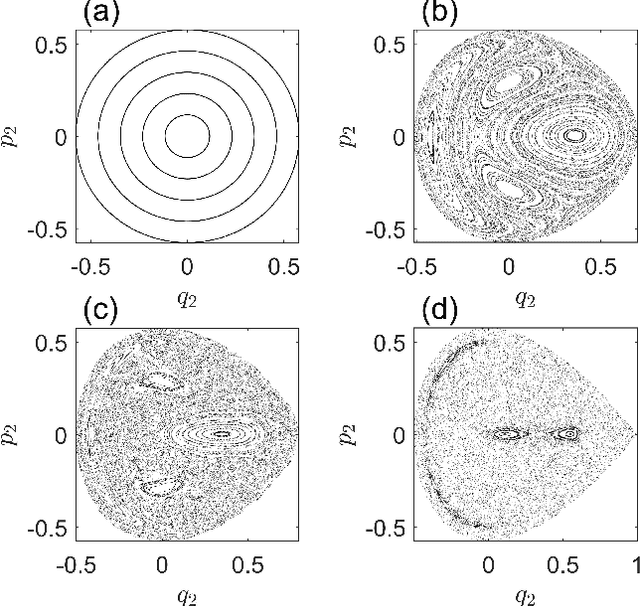
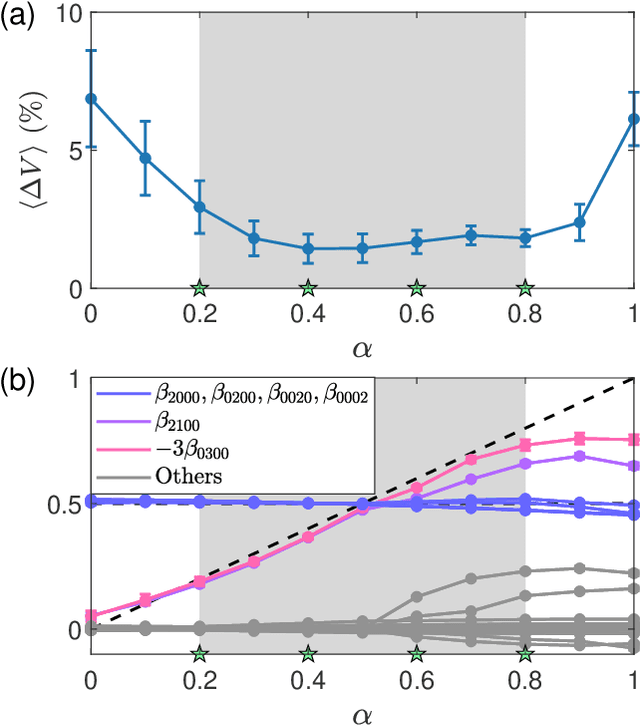
The rapid growth of research in exploiting machine learning to predict chaotic systems has revived a recent interest in Hamiltonian Neural Networks (HNNs) with physical constraints defined by the Hamilton's equations of motion, which represent a major class of physics-enhanced neural networks. We introduce a class of HNNs capable of adaptable prediction of nonlinear physical systems: by training the neural network based on time series from a small number of bifurcation-parameter values of the target Hamiltonian system, the HNN can predict the dynamical states at other parameter values, where the network has not been exposed to any information about the system at these parameter values. The architecture of the HNN differs from the previous ones in that we incorporate an input parameter channel, rendering the HNN parameter--cognizant. We demonstrate, using paradigmatic Hamiltonian systems, that training the HNN using time series from as few as four parameter values bestows the neural machine with the ability to predict the state of the target system in an entire parameter interval. Utilizing the ensemble maximum Lyapunov exponent and the alignment index as indicators, we show that our parameter-cognizant HNN can successfully predict the route of transition to chaos. Physics-enhanced machine learning is a forefront area of research, and our adaptable HNNs provide an approach to understanding machine learning with broad applications.