Deficiency of equation-finding approach to data-driven modeling of dynamical systems

Finding the governing equations from data by sparse optimization has become a popular approach to deterministic modeling of dynamical systems. Considering the physical situations where the data can be imperfect due to disturbances and measurement errors, we show that for many chaotic systems, widely used sparse-optimization methods for discovering governing equations produce models that depend sensitively on the measurement procedure, yet all such models generate virtually identical chaotic attractors, leading to a striking limitation that challenges the conventional notion of equation-based modeling in complex dynamical systems. Calculating the Koopman spectra, we find that the different sets of equations agree in their large eigenvalues and the differences begin to appear when the eigenvalues are smaller than an equation-dependent threshold. The results suggest that finding the governing equations of the system and attempting to interpret them physically may lead to misleading conclusions. It would be more useful to work directly with the available data using, e.g., machine-learning methods.

Unsupervised learning for anticipating critical transitions

For anticipating critical transitions in complex dynamical systems, the recent approach of parameter-driven reservoir computing requires explicit knowledge of the bifurcation parameter. We articulate a framework combining a variational autoencoder (VAE) and reservoir computing to address this challenge. In particular, the driving factor is detected from time series using the VAE in an unsupervised-learning fashion and the extracted information is then used as the parameter input to the reservoir computer for anticipating the critical transition. We demonstrate the power of the unsupervised learning scheme using prototypical dynamical systems including the spatiotemporal Kuramoto-Sivashinsky system. The scheme can also be extended to scenarios where the target system is driven by several independent parameters or with partial state observations.

Reconstructing dynamics from sparse observations with no training on target system

In applications, an anticipated situation is where the system of interest has never been encountered before and sparse observations can be made only once. Can the dynamics be faithfully reconstructed from the limited observations without any training data? This problem defies any known traditional methods of nonlinear time-series analysis as well as existing machine-learning methods that typically require extensive data from the target system for training. We address this challenge by developing a hybrid transformer and reservoir-computing machine-learning scheme. The key idea is that, for a complex and nonlinear target system, the training of the transformer can be conducted not using any data from the target system, but with essentially unlimited synthetic data from known chaotic systems. The trained transformer is then tested with the sparse data from the target system. The output of the transformer is further fed into a reservoir computer for predicting the long-term dynamics or the attractor of the target system. The power of the proposed hybrid machine-learning framework is demonstrated using a large number of prototypical nonlinear dynamical systems, with high reconstruction accuracy even when the available data is only 20% of that required to faithfully represent the dynamical behavior of the underlying system. The framework provides a paradigm of reconstructing complex and nonlinear dynamics in the extreme situation where training data does not exist and the observations are random and sparse.

Kolmogorov-Arnold Network Autoencoders

Deep learning models have revolutionized various domains, with Multi-Layer Perceptrons (MLPs) being a cornerstone for tasks like data regression and image classification. However, a recent study has introduced Kolmogorov-Arnold Networks (KANs) as promising alternatives to MLPs, leveraging activation functions placed on edges rather than nodes. This structural shift aligns KANs closely with the Kolmogorov-Arnold representation theorem, potentially enhancing both model accuracy and interpretability. In this study, we explore the efficacy of KANs in the context of data representation via autoencoders, comparing their performance with traditional Convolutional Neural Networks (CNNs) on the MNIST, SVHN, and CIFAR-10 datasets. Our results demonstrate that KAN-based autoencoders achieve competitive performance in terms of reconstruction accuracy, thereby suggesting their viability as effective tools in data analysis tasks.

Machine-learning prediction of tipping and collapse of the Atlantic Meridional Overturning Circulation

Recent research on the Atlantic Meridional Overturning Circulation (AMOC) raised concern about its potential collapse through a tipping point due to the climate-change caused increase in the freshwater input into the North Atlantic. The predicted time window of collapse is centered about the middle of the century and the earliest possible start is approximately two years from now. More generally, anticipating a tipping point at which the system transitions from one stable steady state to another is relevant to a broad range of fields. We develop a machine-learning approach to predicting tipping in noisy dynamical systems with a time-varying parameter and test it on a number of systems including the AMOC, ecological networks, an electrical power system, and a climate model. For the AMOC, our prediction based on simulated fingerprint data and real data of the sea surface temperature places the time window of a potential collapse between the years 2040 and 2065.

Random forests for detecting weak signals and extracting physical information: a case study of magnetic navigation

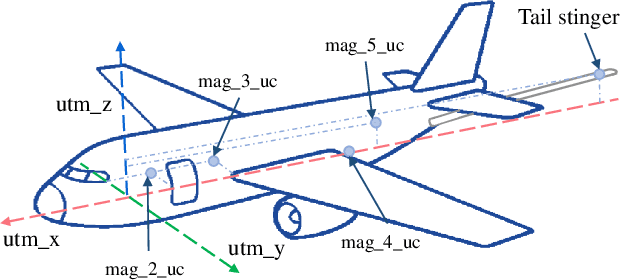
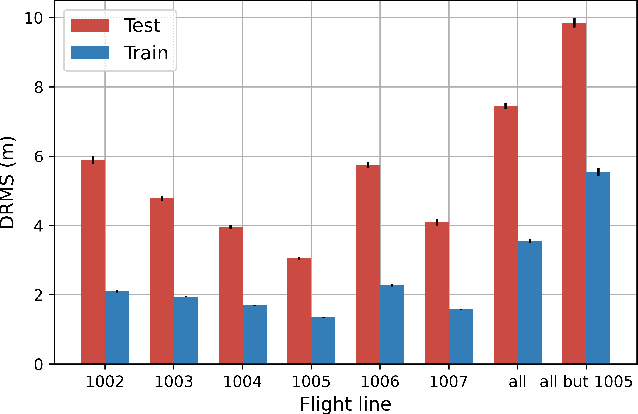
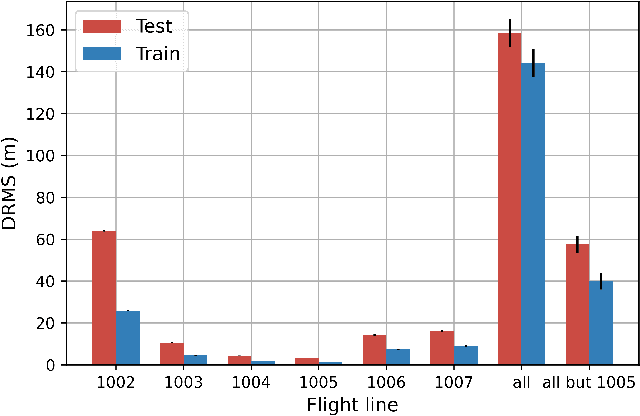
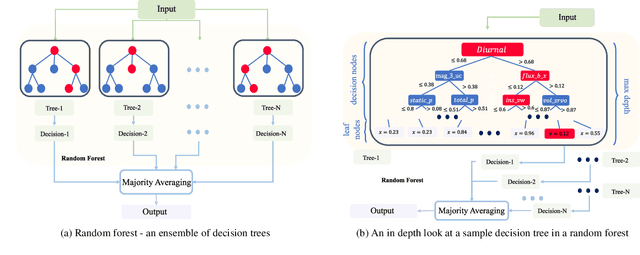
It was recently demonstrated that two machine-learning architectures, reservoir computing and time-delayed feed-forward neural networks, can be exploited for detecting the Earth's anomaly magnetic field immersed in overwhelming complex signals for magnetic navigation in a GPS-denied environment. The accuracy of the detected anomaly field corresponds to a positioning accuracy in the range of 10 to 40 meters. To increase the accuracy and reduce the uncertainty of weak signal detection as well as to directly obtain the position information, we exploit the machine-learning model of random forests that combines the output of multiple decision trees to give optimal values of the physical quantities of interest. In particular, from time-series data gathered from the cockpit of a flying airplane during various maneuvering stages, where strong background complex signals are caused by other elements of the Earth's magnetic field and the fields produced by the electronic systems in the cockpit, we demonstrate that the random-forest algorithm performs remarkably well in detecting the weak anomaly field and in filtering the position of the aircraft. With the aid of the conventional inertial navigation system, the positioning error can be reduced to less than 10 meters. We also find that, contrary to the conventional wisdom, the classic Tolles-Lawson model for calibrating and removing the magnetic field generated by the body of the aircraft is not necessary and may even be detrimental for the success of the random-forest method.

Machine-learning parameter tracking with partial state observation

Complex and nonlinear dynamical systems often involve parameters that change with time, accurate tracking of which is essential to tasks such as state estimation, prediction, and control. Existing machine-learning methods require full state observation of the underlying system and tacitly assume adiabatic changes in the parameter. Formulating an inverse problem and exploiting reservoir computing, we develop a model-free and fully data-driven framework to accurately track time-varying parameters from partial state observation in real time. In particular, with training data from a subset of the dynamical variables of the system for a small number of known parameter values, the framework is able to accurately predict the parameter variations in time. Low- and high-dimensional, Markovian and non-Markovian nonlinear dynamical systems are used to demonstrate the power of the machine-learning based parameter-tracking framework. Pertinent issues affecting the tracking performance are addressed.

Digital twins of nonlinear dynamical systems: A perspective

Digital twins have attracted a great deal of recent attention from a wide range of fields. A basic requirement for digital twins of nonlinear dynamical systems is the ability to generate the system evolution and predict potentially catastrophic emergent behaviors so as to providing early warnings. The digital twin can then be used for system "health" monitoring in real time and for predictive problem solving. In particular, if the digital twin forecasts a possible system collapse in the future due to parameter drifting as caused by environmental changes or perturbations, an optimal control strategy can be devised and executed as early intervention to prevent the collapse. Two approaches exist for constructing digital twins of nonlinear dynamical systems: sparse optimization and machine learning. The basics of these two approaches are described and their advantages and caveats are discussed.

Model-free tracking control of complex dynamical trajectories with machine learning

Nonlinear tracking control enabling a dynamical system to track a desired trajectory is fundamental to robotics, serving a wide range of civil and defense applications. In control engineering, designing tracking control requires complete knowledge of the system model and equations. We develop a model-free, machine-learning framework to control a two-arm robotic manipulator using only partially observed states, where the controller is realized by reservoir computing. Stochastic input is exploited for training, which consists of the observed partial state vector as the first and its immediate future as the second component so that the neural machine regards the latter as the future state of the former. In the testing (deployment) phase, the immediate-future component is replaced by the desired observational vector from the reference trajectory. We demonstrate the effectiveness of the control framework using a variety of periodic and chaotic signals, and establish its robustness against measurement noise, disturbances, and uncertainties.

Generating extreme quantum scattering in graphene with machine learning

Graphene quantum dots provide a platform for manipulating electron behaviors in two-dimensional (2D) Dirac materials. Most previous works were of the "forward" type in that the objective was to solve various confinement, transport and scattering problems with given structures that can be generated by, e.g., applying an external electrical field. There are applications such as cloaking or superscattering where the challenging problem of inverse design needs to be solved: finding a quantum-dot structure according to certain desired functional characteristics. A brute-force search of the system configuration based directly on the solutions of the Dirac equation is computational infeasible. We articulate a machine-learning approach to addressing the inverse-design problem where artificial neural networks subject to physical constraints are exploited to replace the rigorous Dirac equation solver. In particular, we focus on the problem of designing a quantum dot structure to generate both cloaking and superscattering in terms of the scattering efficiency as a function of the energy. We construct a physical loss function that enables accurate prediction of the scattering characteristics. We demonstrate that, in the regime of Klein tunneling, the scattering efficiency can be designed to vary over two orders of magnitudes, allowing any scattering curve to be generated from a proper combination of the gate potentials. Our physics-based machine-learning approach can be a powerful design tool for 2D Dirac material-based electronics.